- +1
中国队遭“团灭”的第三题,我是如何解题的?
编者按:在2月25日的罗马尼亚数学大师赛(RMM)上,难倒中国选手的“第三题”引起热议。近日在“湃客·镜相”栏目独家撰稿、讲述自己数学之路的美国奥数国家队主教练罗博深(Po-shen Loh)及其编辑团队在其公众号上提供了题目解法,并授权“湃客·众声”栏目转载。本文分为通俗版、简略版和英文完整版,供不同程度的读者参考,中文完整版将在之后发布。本文首发于“罗博深数学”公众号:LuoboshenMath。
通俗版
作者、编辑|罗数君
全网火热的一道数学题,“难倒中国选手的第三题”,今天就让罗教授告诉你到底怎么解——
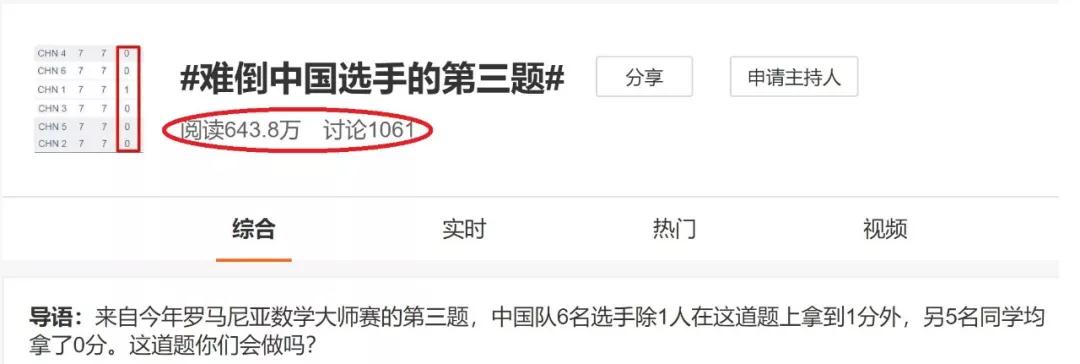
万年上不了热搜的数学话题
这次居然在微博上引起了不小的讨论


足以媲美三线小明星的八卦了
罗数君定睛一看,原来和今年的
罗马尼亚数学大师杯(RMM)有关
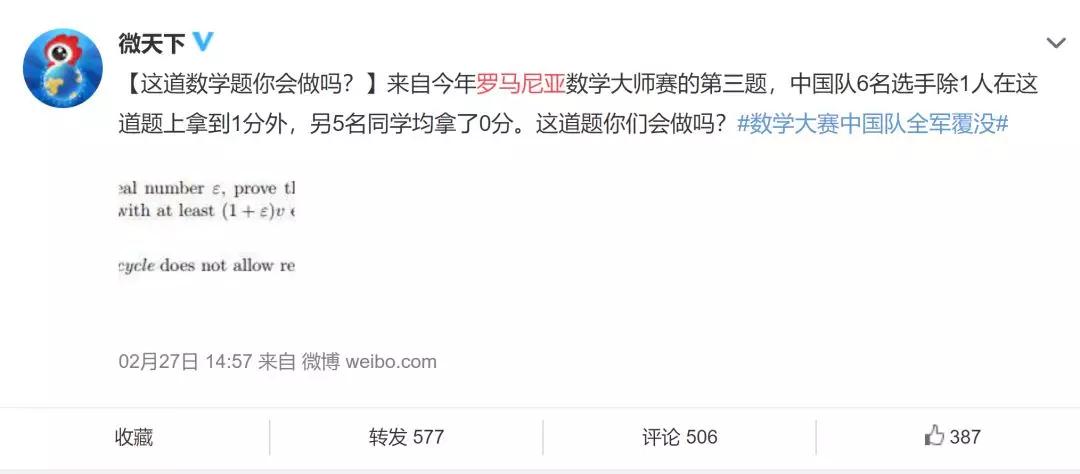
尤其是那“难倒中国选手的第三题”
一时间关于这道题的讨论层出不穷


这道题的难度非同小可——
金牌和银牌的差距
几乎全在能否解出这道题上

罗数君隔着屏幕
仿佛看到了大家求知若渴的眼神
当下不敢怠慢,立刻去请教了罗教授
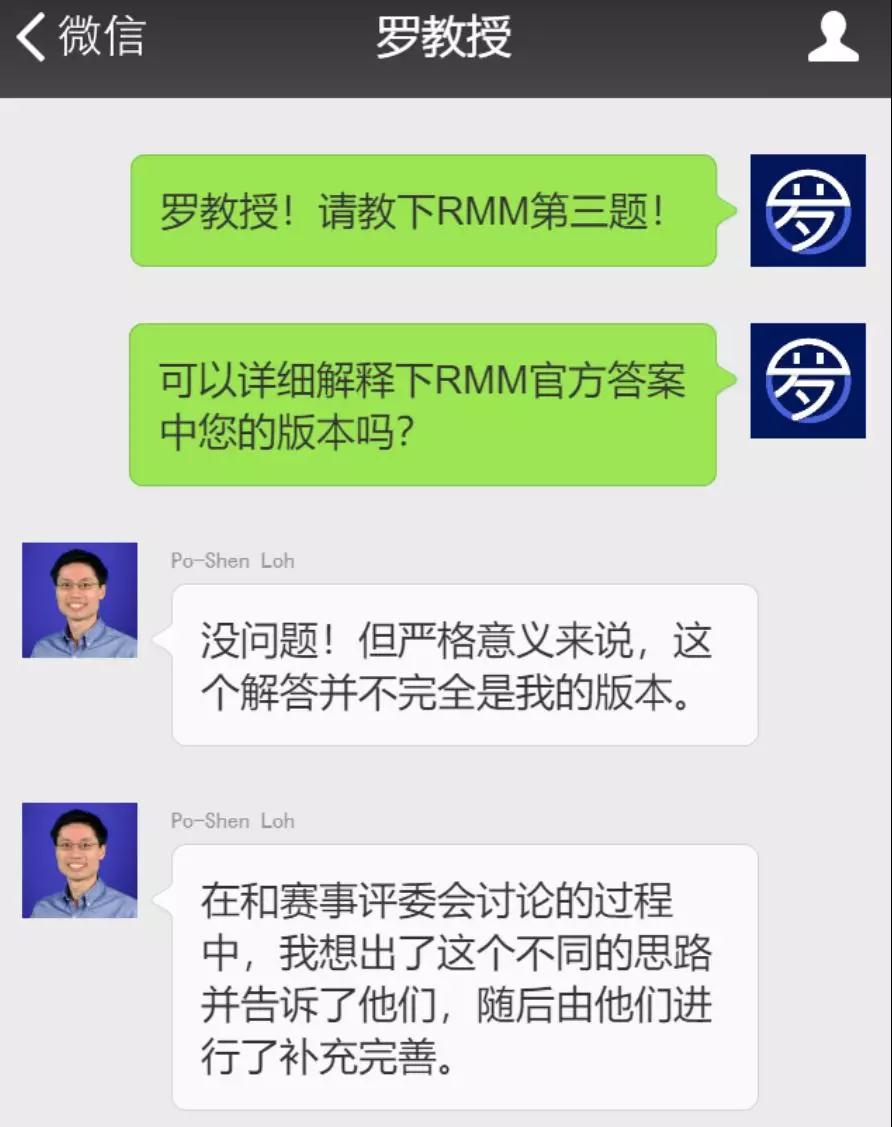
第三题有两种解法,一种是官方的
另一种则署了罗教授的名字
但罗教授谦虚地表示
这个版本的回答他只是提供了思路
随后的推理证明由赛事组委会完成
但可能对于许多非数学专业的朋友来说,光读题就已经让人感觉怀疑人生了……


本题题目:给定任意正实数ε,请证明,除了有限个反例之外,所有正整数v都满足:所有由v个顶点和至少(1+ ε)v条边构成的图,都存在一对等长的不同简单圈(注意,简单圈不允许重复出现相同的顶点)。
但看到这道题目的时候,我们很容易被题目中图论的概念吓住,因为在初高中的学习中,我们很少提到图论,也很少会花时间了解图论中不同术语的概念。但其实中学生学习图论也大有裨益。
回到题目。其实通过一些简单的介绍,很快我们就能帮同学们看明白这个问题,并且找到解题灵感。
首先,让我们了解一下这道题目中出现的图论的术语:
顶点(vertex):图论中图(graph)的基本组成部分是顶点(vertex)和连接顶点的边(edge)
边(edge):连接两个顶点的线叫边(edge)
圈(cycle):图论中,圈从一个顶点起步,沿着不重复的边,不重复的顶点为途径,回到起点的闭合路径。

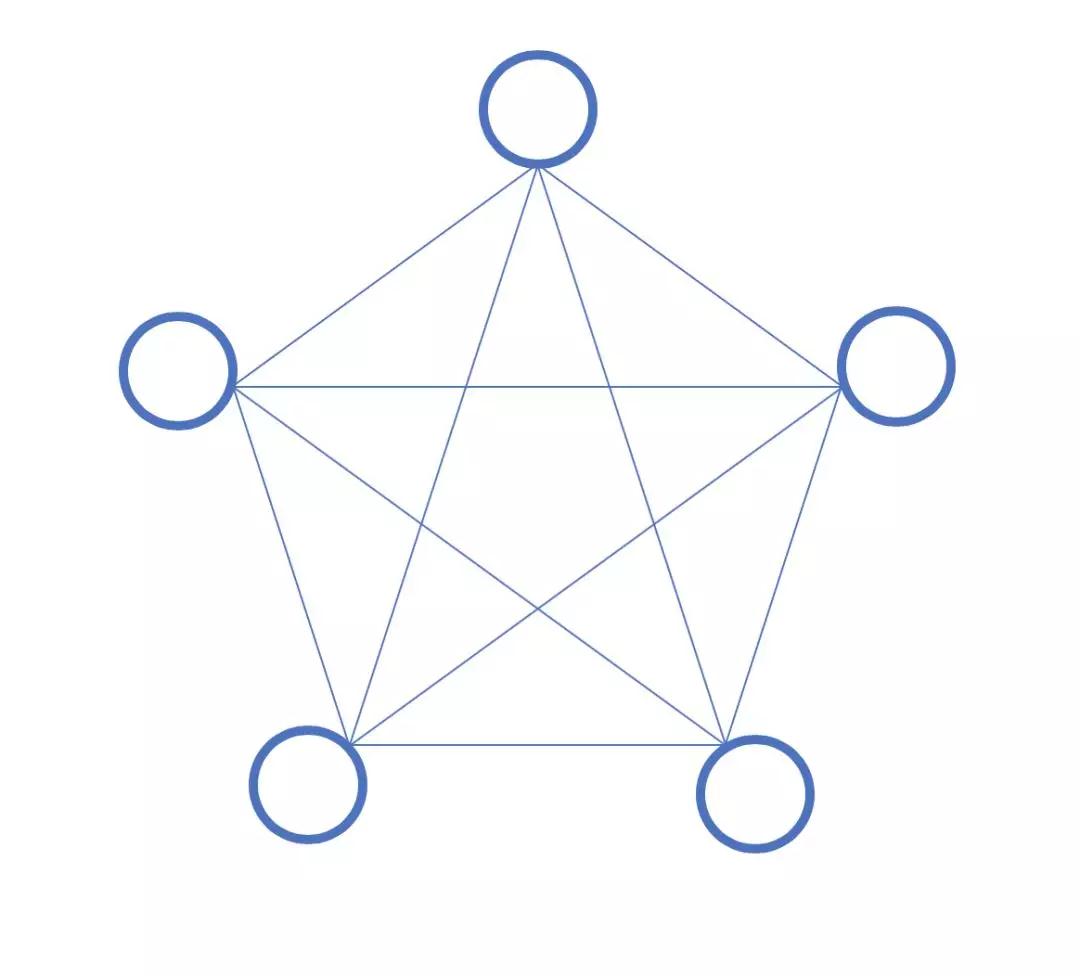

现在,让我们思考一个稍难一点的问题:在一个有n个顶点且不存在圈的图中,最多能有多少条边?
我们不难想出,在一个有n个顶点的图中,如果已经存在了n-1个边,增加的任意一条边都会让这个图产生一个圈。我们可以通过下图来看一看:

我们可以看出,当一个图的边越多,这个图中不一样的圈也会越来越多。现在,我们就可以更好的理解RMM的这个问题。当一个图中有v个顶点,且有(1+ ε)v条边,因为ε大于0,这个图中边的数量一定>v,我们不难知道这个图中将会存在一些圈。这道题目的核心,就是证明出在这些图中,我们能找到两个长度相同的圈。
看懂题目了吗?恭喜你,完成了解决这道题目最简单的部分!接下来更难的部分自然是后续的推理证明了。当然了,对题目理解越深,就会有越多的解题思路和灵感。

问题3是整个比赛中最具数学趣味性的,也是最吸引我的部分。我受到一些组合学研究的启发,想出了一种解决方案。我还打算把这个问题带回去给我的博士学生,这是非常有趣的研究点。
我认为解出问题3的关键,在于对数学理念有更深层次的理解和思考。我建议在培养学生的数学能力时,既要发展高阶数学思维,同时也要用做题巩固训练;这是训练IMO的一种创新,也是一种新的挑战。
美国队员们经常聚到一起讨论研究相关的数学话题。这样的经历让他们可以更好地思考这类问题。我发现很多国家队教练都在朝这个方向转变观念。近几年,国际数学竞赛的题目开始有越来越多数学研究的影子,我们也可以预见这样的题目会被更多人认可。

就现在来看,除了满足数学爱好者的“探索精神”外,可能“毫无用处”。
但当费马潜心研究数论的时候,绝对不会想到如今它在密码学中的举足轻重;当高斯在钻研统计学、线性代数的时候,也不会想到它们如今成为了机器学习的基石。
有人说数学太虚无,又有人说数学最真实。一万个数学爱好者里有一万种数学,但它们都有一个最共同的特点——他们都深爱着数学。
简略版
作者|Peter
编辑|罗数君
本答案是RMM官方答案中,署名罗教授版本的翻译版。由罗教授提供思路,RMM官方委员会进行推理论证,罗博深数学实习生Peter进行翻译、注释。
题目:Given any positive real number ε, prove that, for all but finitely many positive
integers v, any graph on v vertices with at least(1 + ε)v edges has two distinct simple cycles of equal lengths.
给定任意正实数ε,请证明,除了有限个反例之外,所有正整数v都满足:所有由v个顶点和至少(1 +ε)v 条边构成的图,都存在一对等长的不同简单圈(注意,简单圈不允许重复出现相同的顶点)。
注:本证明旨在帮助大家理解题目背后的思想,因此省略了很多严谨的细节。如果你不满足于这篇概要,欢迎访问RMM官网(http://rmms.lbi.ro/rmm2019/index.php?id=problems_math)查看完整的证明。如果有其他疑问,欢迎在文章下留言,我们会尽全力解答的哦~
在开始证明之前,我们先来介绍几个图论中基本的概念:
顶点(vertex):图论中图(graph)的基本组成部分是顶点(vertex)和连接顶点的边(edge)
边(edge):连接两个顶点的线叫边(edge)
相邻(adjacent):如果两个顶点之间存在一条边,我们说它们是相邻的。
度数(degree):对于任何一个顶点v,与它相临的所有顶点的总数叫做这个顶点的度数, 用deg(v)表示。
邻域(neighborhood):对于任何一个顶点v,与它相临的所有顶点组成的集合叫做v的邻域,用N(v)表示。
路径(path):图论中,路径的本质是一个顶点序列,它的每个顶点有一条边连接该序列中下一顶点。一条路径可能是无穷的,但有限路径有一个最先顶点,称为起点,和最后顶点,称为末点,这两个顶点都叫做端点。
圈(cycle):图论中,圈从一个顶点起步,沿着不重复的边,不重复的顶点为途径,回到起点的闭合路径。
连通性(connectedness):如果对于图中的任何两个顶点,我们都能找到一条路径以它们为两个端点,那我们说这个图是联通的。
树(tree):如果图符合以下标准:
1.边的数量是顶点数量减一 2.图是联通的3.图中不存在圈
我们说这幅图是树。
环(loop):一条连接顶点本身的边
围长(girth):图中最短圈包含的边数,比如一个正方形的围长就是4
Little o: f(n) = o(g(n)) 当且仅当对于任意c > 0和n ≥ k ,存在正实数k,使得0 ≤ f(n) < cg(n) 。k 的取值与n无关, 但可以与c相关。
引理:任意固定的正实数δ,都满足:在v个顶点上,且围长至少为δv的图,最多有v+ o(v)条边。
证明:




作者|罗博深
编辑|罗数君

Problem 3. Given any positive real number ε, prove that for all but finitely many positive integers N, any simple graph on N vertices with at least (1+ε)N edges has two different simple cycles of equal length.
(A simple graph is a set V of vertices, together with a set E of edges, where each edge in E is a set of two vertices of V. A simple cycle of length K is a set C of K ≥ 3 distinct edges in E, such that there is a sequence of distinct vertices v1, v2, …, vK such that for each 1 ≤ i < K, {vi, vi+1} is in C, and {vk, v1} is in C.)
The official reference shows the original statement of this problem:
http://rmms.lbi.ro/rmm2019/index.php?id=problems_math
Here, I will explain the “sketch of solution 2” on the final page of that document which is attributed to me. Indeed, I thought this was the most interesting question on the entire paper, because it had research flavor. It is closely related to a field of active research, called extremal combinatorics, which is also my area of specialization. During the time that the national coaches were thinking about the exam problems, I focused on this one, and discovered an intuitive alternative solution, which is close to the best possible dependency between ε and the first N that works for that ε. This solution may look long, but that is because I am pointing out the intuition behind each step, instead of simply saying how it works.
Start by considering an arbitrary graph in which all simple cycles have different lengths, but which has at least (1+ε)N edges. We seek a contradiction for all sufficiently large N. Find the shortest cycle, and delete one of its edges. In this new graph, the shortest cycle is not the same as the previous shortest cycle, because one edge has been deleted. Since all cycle lengths are different, the shortest cycle is now strictly longer. Find it, and delete one of its edges. The length of the shortest cycle in the new graph is even larger. Therefore, after repeating this process εN/2 times, we will reach a graph which still has at least (1+(ε/2))N edges, but there are no cycles of length εN/2 or shorter. The technical term for this is the girth of a graph, which is the length of the shortest cycle in the graph. Therefore, it suffices to prove the following lemma (where we rescaled ε to produce a more elegant statement).
Lemma. Given any positive real number ε, prove that for all but finitely many positive integers N, any simple graph on N vertices with at least (1+ε)N edges has a cycle of length shorter than εN.
When I realized this, I knew I was not far from the solution, because cycles start to appear as soon as the number of edges rises to reach the number of vertices, and once there are many cycles, they start to intersect (creating more cycles), making it impossible to have only cycles of length at least linear in N. The rest of the solution may look very long, but it is actually a natural consequence of several intuitive steps:
(1) define a function to track the relationship between vertices, girth, and edges, (2) proceed by contradiction, using the minimum cycle length condition to find enormous trees in the graph, (3) deduce that the trees must have long paths without branching, or else they would use far too many vertices, (4) delete the long paths one by one, significantly reducing the total number of vertices at each stage while only increasing the difference between the numbers of edges and vertices by +1, and (5) show that the number of such stages is too small, contradicting the size of the assumed difference between numbers of edges and vertices.
We now proceed to prove the lemma in detail. The key idea is to use the following concept which is common in research combinatorics.
Definition. The excess of a graph is defined to be E − V + 1, where E is the number of edges and V is the number of vertices.
This is a useful definition because of the basic and well-known fact that it is possible for a graph with V vertices and E = V − 1 edges to have no cycles, but as soon as the number of edges reaches V, there is at least one cycle. In other words, there are graphs with excess 0 which have no cycles, but every graph with excess greater than zero definitely contains at least one cycle. When studying cycles in graphs, it is often more convenient to reason in terms of the excess rather than to reason in terms of the numbers of edges and vertices. Formulas are often much simpler. This motivates the definition of a very natural function, which is a reasonable function to study from a research perspective. (Indeed, when I reached this point, I felt that surely this precise function must already have been studied before by researchers, and that piqued my interest.)
Definition. Let F(N, g) denote the maximum excess of a graph which has N vertices and girth at least g (having no cycles of length less than g).
In terms of this definition, we can prove the Lemma by showing that for all sufficiently large N, we have F(N, εN) ≤ εN. The intuition is to upper-bound this evaluation of F in terms of evaluations of F with smaller parameters (recursive thinking).
So, consider an arbitrary graph G with N vertices, which has no cycles of length less than εN, but maximizes the excess subject to these conditions. Then G must have excess exactly F(N, εN). We consider several cases.
Case 1. Graph G has at least one vertex U of degree 1.
Delete vertex U, to obtain a new graph G’ with N − 1 vertices. It still has no cycles of length less than εN, because deleting an edge cannot create any cycles. Since U has degree 1, the excess of G’ is exactly the same as F(N, εN) (the excess of G). Yet the excess of G’ is less than or equal to F(N−1, εN), so we conclude that in this case: F(N, εN) ≤ F(N−1, εN).
Case 2. Graph G has no vertices of degree 1.
We now use the fact that there are no cycles of length less than εN, via the standard argument of considering an arbitrary vertex U of degree greater than 0, and considering the subgraph H of G induced by all vertices which are at distance up to (εN/2)−1 from U. Crucially, H is a tree, because if any two vertices Y and Z in H were adjacent, then it would be possible to walk from Y to U to Z and back to Y in less than or equal to ((εN/2)−1) + ((εN/2)−1) + 1 < εN steps, contradicting the fact that G has no cycles of length less than εN.
However, H is a very strange tree. It cannot have more than N vertices, because G has N vertices. Yet at the same time, it has a depth of about εN/2 from its root U, which is quite long. (For the remainder of this solution, my calculations will be off by lower order terms to simplify the presentation. For example, I will make calculations in terms of εN/2 instead of (εN/2)−1. This does not substantially change the nature of the asymptotic bounds.) Visualize the tree H exploding from its root U. There are no vertices of degree 1, and we will never reach a vertex of degree 0 because we are following along paths from U. Vertices of degree 3 and higher cause a chain reaction creating more and more branches, which will cause trouble because we cannot surpass N vertices. This suggests that as we travel away from U, much time is spent on long paths of degree 2, which do not create any further expansion. We want to show that there is a fairly long such path, so that we can use it to finish the problem another major step later.
So, let M be the maximum number of consecutive degree-2 vertices in a path in G. For each T = 0, 1, 2, 3, …, (εN/2)−1, think of the set ST of vertices which are exactly T steps away from U along the tree H. This looks like a wave expanding away from U. Since there are no vertices of degree 1, every vertex in ST either corresponds to exactly one vertex in ST+1 (if it had degree 2), or creates multiple vertices in ST+1 (if it had degree 3 or higher). This is similar to a bacterial multiplication process, in which you start at T=0 with one bacterium, and when moving to each new time step, each existing bacterium either remains or multiplies. Crucially, the time period between multiplications is less than or equal to (about) M. So, after T reaches (about) εN/2, we must finish with at least (about)
2^( (εN)/(2M) )
vertices in the final ST. This lower bound comes from considering the worst case scenario, in which every multiplication is simply from a degree-3 vertex (one edge coming from the direction of U, and two edges going in the direction of the next S), in which case every bacterium multiplies by exactly 2.
However, there are only N vertices altogether, and therefore we obtain the inequality:
N ≥ 2^( (εN)/(2M) )
Let lg() denote the base-2 logarithm. Then, we have:
lg(N) ≥ (εN)/(2M)
which implies:
M ≥ (εN)/(2 lg(N)),
i.e., that there is a path in G of at least (εN)/(2 lg(N)) many degree-2 vertices. Intuitively, this is rather large, because lg(N) grows very slowly compared to N.
Now consider the graph G’ obtained by deleting those M vertices and the M+1 edges incident to them. This new graph still has no cycles of length less than εN, and so its excess must be less than or equal to F(N−M, εN). At the same time, since exactly one more edge than vertex was deleted, the excess of G’ is exactly F(N, εN) − 1 (recall F(N, εN) was the excess of G). Therefore,
F(N, εN) − 1 ≤ F(N−M, εN)
which implies that
F(N, εN) ≤ F(N−M, εN) + 1,
with a particular value of M that is at least (εN)/(2 lg(N)). This completes Case 2.
To finish this proof, recall that the conclusion of Case 1 was that F(N, εN) ≤ F(N−1, εN). Observe that in both cases, we obtain an upper bound for F(N, εN) in terms of an evaluation of F with a smaller first parameter (number of vertices), possibly with a +1 at the end. We can repeat this argument enough times until the number of vertices shrinks down to a convenient value.
In particular, it is easy to see that for any K < L, we have F(K, L) = 0, because in any graph which has K < L vertices, if there are no cycles of length less than L, that means there are actually no cycles of any length at all, which means that the maximum excess is 0 (achieved by a tree).
So, F(N, εN) is actually less than or equal to the number of times we do the +1 (Case 2) step, as we reduce the first parameter (number of vertices) until that first parameter falls below εN, because that final F(N’, εN) with N’ < εN is actually 0. Each Case 2 step corresponds to reducing the first parameter by at least about (εN)/(2 lg(N)). This bound holds even in later iterations because the number N’ of vertices will shrink below N, but the girth condition will remain at εN, and conveniently the only change to the bound on M when N’ is used is M ≥ (εN)/(2 lg(N’)), which is still at least (εN)/(2 lg(N)). Therefore, within about (2 lg(N))/ε Case 2 steps, the first parameter would hit 0, implying that it would definitely fall below εN within (2 lg(N))/ε Case 2 steps. Each Case 2 step contributes a +1, so F(N, εN) ≤ (2 lg(N))/ε, which for sufficiently large N is much better than the required bound of F(N, εN) ≤ εN.
If this argument is run more carefully, it can even be used to prove that there is a function f(N) which has asymptotic order of magnitude sqrt(N log(N)), such that any simple graph on N vertices with at least N + f(N) edges has two different simple cycles of equal length.
(本文首发于“罗博深数学”公众号:LuoboshenMath。)
本文为澎湃号作者或机构在澎湃新闻上传并发布,仅代表该作者或机构观点,不代表澎湃新闻的观点或立场,澎湃新闻仅提供信息发布平台。申请澎湃号请用电脑访问http://renzheng.thepaper.cn。




- 报料热线: 021-962866
- 报料邮箱: news@thepaper.cn
互联网新闻信息服务许可证:31120170006
增值电信业务经营许可证:沪B2-2017116
© 2014-2024 上海东方报业有限公司




