弹性力学中主矢量及主矩正负号的统一表达

原创 刘章军 阮鑫鑫 物理与工程

摘 要

在弹性力学中，由于未明确给出主矢量和主矩的正负号统一规定，在分析不同的问题时容易产生混淆。为此，首先考察材料力学中内力的正负号规定，并详细剖析在不同坐标系下材料力学中内力正负号规定所导致的差异性。同时，建议弹性力学中用应力分量来定义主矢量和主矩的正负号，从而实现材料力学与弹性力学问题解答的一致性。最后，通过对 4 个弹性力学典型应用实例的分析，进一步阐明所建议的主矢量和主矩正负号规定的统一性。实践表明，该统一表达可有效帮助学生理解力学概念，分析力学问题，教学效果显著。

关键词 弹性力学；材料力学；主矢量及主矩；正负号；统一表达

Abstract In elastic mechanics, since the signs of principal vector and principal moment are not clearly specified, it is easy to be confused when analyzing different problems. To this end, first of all, the signs of internal force in material mechanics are investigated carefully, and the differences brought by the signs of internal force in material mechanics under different coordinate systems are analyzed. Meanwhile, it is recommended to use stress components to define the signs of principal vectors and principal moments in elastic mechanics, so as to achieve consistency between material mechanics and elastic mechanics solutions. Finally, through the analysis of four typical examples in elastic mechanics, the unity of the signs associated with the proposed principal vector and principal moment is further clarified. Practice shows that the unified expression can effectively help students understand the concept of mechanics and analyze mechanics problems, and the teaching effect is remarkable.

力学教学中常常会遇到用正号还是负号表述的纠结[1]，专业物理力学教师对此尚且能够理解，但对于初学物理力学课程的学生而言，则更需要清晰一致的表述来加强他们对物理力学概念的理解。由于材料力学中已经明确规定了内力主矢量及主矩的正负号[2,3]，因此，应该直接采用材料力学中的正负号规定，还是重新定义主矢量和主矩的正负号，是弹性力学教学实践中经常面临的一个困扰[4]。一方面，弹性力学中基本物理量的正负号规定，有的与材料力学相同，有的又不完全相同，例如，正应力分量的正负号规定相同，但切应力分量的正负号规定不完全相同[5]；同时，在弹性力学的一些问题中对此具有专门的定义，例如，薄板弯曲问题中的内力正负号规定[6]，这就使得弹性力学关于内力和外力的主矢量及主矩的正负号规定很不统一，令人混淆。另一方面，在比较材料力学解答与弹性力学解答的差异性时，又必须考虑弹性力学与材料力学关于应力分量以及内力正负号规定的一致性问题，进而带来诸多不便。

鉴于此，本文首先仔细考察了材料力学中内力正负号规定的优缺点，并深入剖析不同坐标系下材料力学内力正负号规定所带来的差异性，以及产生其差异性的原因。在此基础上，针对弹性力学研究对象的复杂性，提出了用应力分量的正负号规定来定义内力以及外力的主矢量和主矩的正负号，从而使得不同的弹性力学问题能够得到统一处理，同时也有效地解决了弹性力学解答与材料力学解答的一致性问题。

1 材料力学中内力的正负号规定

在材料力学中，通常根据变形特征来规定内力的正负号。例如，教材[2]、[3]给出了轴力、扭矩、剪力和弯矩的正负号规定，具体如下：轴力是以引起轴向伸长变形时为正，扭矩是以使杆的纵向线在某一段内有变成右手螺旋线的趋势时为正，剪力是以引起 dx 微段有左端向上而右端向下的相对错动时为正，弯矩是以引起 dx 微段的下半部纵向受拉时为正；反之为负。材料力学关于内力主矢量及主矩的正负号规定，其合理性主要体现在 3 个方面：一是直观地将内力与自身的变形联系在一起，便于建立力学概念；二是体现了作用与反作用原理以及右手螺旋法则，例如，扭矩也可以按右手螺旋法则来定义其正负号；三是由内力的正负号规定可以直接延伸到杆端边界处外力主矢量及主矩的正负号规定，这样在直杆两端上外力主矢量及主矩的正方向刚好相反。

然而，材料力学关于内力和杆端外力的主矢量及主矩的正负号规定，未能与坐标系联系起来，因而不能反映数学逻辑关系，这为材料力学后续学习带来一定的不便。例如，在研究梁弯曲的位移时，由于挠度、转角以及曲率均与坐标系有关，其正负号是在给定的坐标系下规定的。为了清晰地阐明这一点，以材料力学中矩形截面简支梁受均布荷载 q0 的弯曲为例，其中取梁的截面宽度 b=1，忽略梁的自重。现去掉支座而直接用支反力代替，对于图 1 和图 2 所示的两种坐标系，按照材料力学中内力和杆端外力的主矢量及主矩的正负号规定来分析，其中梁两端的剪力均已按正向来表示。

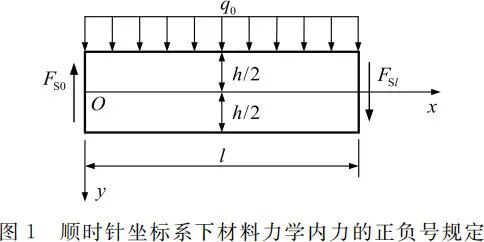
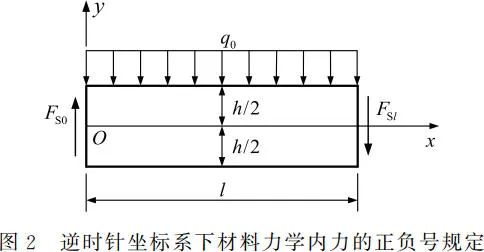根据平衡条件，图 1 和图 2 中梁左端的剪力

，右端剪力

。同时，图 1 和图 2 的横截面内力（弯矩和剪力）也都相同，即

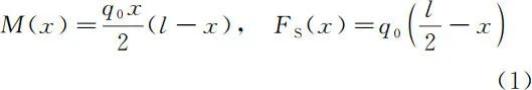在图 1 的坐标系下，材料力学梁弯曲的基本公式和挠曲线近似微分方程分别为[2]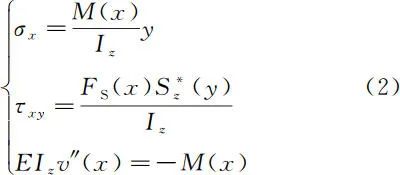其中，Iz 为横截面对中性轴 z 的惯性矩，

为横截面上距中性轴为 y 的横线以外部分的面积对中性轴 z 的静距，E 为材料的弹性模量，v(x) 为横截面的挠度。

在图 2 的坐标系下，材料力学的基本公式和挠曲线近似微分方程则为[3]

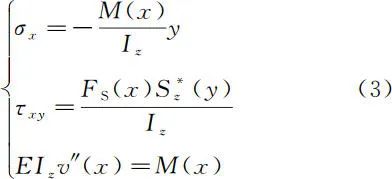于是，将式（1）代入式（2）的前两式中，即可得到图 1 坐标系下的正应力 σx 和切应力

。同样地，将式（1）代入式（3）的前两式中，得到图 2 坐标系下的正应力 σx 和切应力

。

这表明，在图 1 和图 2 所示的两种坐标系下，梁截面上的内力（弯矩和剪力）完全相同，而材料力学梁弯曲的基本公式不完全相同，挠曲线近似微分方程也不相同，而相差一个负号。事实上，导致这种差异性的原因在于挠度、转角及曲率是按数学方式来规定其正负号，即挠度始终以沿 y 轴正向时为正，转角以从 x 轴正向转向 y 轴正向时为正；而内力的正负号则是以变形特征来规定的，并没有按数学方式来规定。

2 弹性力学中主矢量及主矩的正负号规定

如前所述，在弹性力学的教材中并未明确给出内力和外力的主矢量及主矩的正负号规定，对于某些情况，可能会因主矢量及主矩的正负号规定不统一而带来混淆，甚至导致错误。为统一起见，在弹性力学中，应当按照应力分量的正负号规定来定义内力和外力主矢量及主矩的正负号。事实上，由于应力分量的正负号规定是以正面正向为正，负面负向为正，反之为负，这样不仅可以与坐标系有机结合来体现数学的逻辑关系，而且能够正确地反映作用与反作用原理。

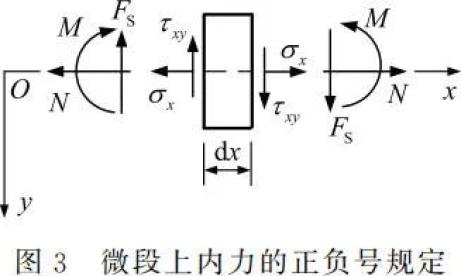
对于内力主矢量及主矩的正负号规定，以平面问题为例，如图 3 所示，轴力 N、剪力 FS 和弯矩 M 的正负号规定是从应力分量的正负号规定得出的，即：轴力 N 以截面上产生正号的正应力 σx 时为正，反之为负；剪力 FS 以截面上产生正号的切应力

为正，反之为负；弯矩 M 以截面上 y > 0 的一侧产生正号的正应力 σx 为正，反之为负。同时，根据应力分量定义的内力主矢量及主矩的正负号，可以方便地延伸到端部边界上的已知主矢量和主矩的正负号规定，如图 4 所示。这样，就实现了微段与端部的主矢量和主矩正负号的统一规定，即实现内力与外力正负号的统一规定。

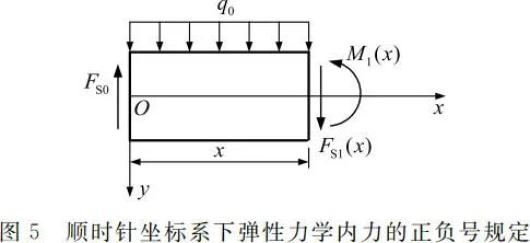
显然，对于第 1 种坐标系（按右手螺旋法则，图 1 坐标系的大拇指是指向屏幕内），按照应力分量来定义的主矢量及主矩正负号与材料力学所规定的完全一致；对于第 2 种坐标系（按右手螺旋法则，图 2 坐标系的大拇指是指向屏幕外），按照应力分量来定义的主矢量及主矩正负号与材料力学所规定的正好相反。可见，用应力分量的正负号规定来定义内力和外力的主矢量及主矩的正负号，就可以体现坐标轴方向的改变对主矢量及主矩的正负号影响。下面，按照上述弹性力学关于内力和端部外力的正负号规定，重新分析图 1 和图 2 所示坐标系下的梁弯曲问题。

对于图 1 坐标系下的梁弯曲问题，若按照弹性力学关于内力的正负号规定（见图 5），其中左端剪力

，横截面的内力为

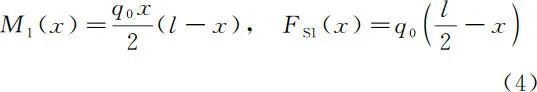
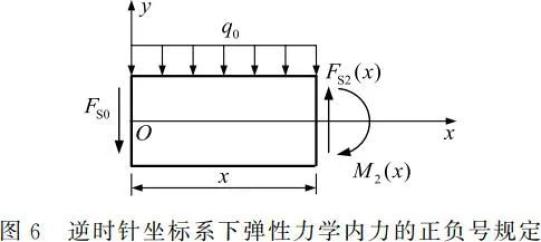
对于图 2 坐标系下的梁弯曲问题，按照弹性力学关于内力的正负号规定（见图 6），其中左端剪力

，横截面的内力应当为

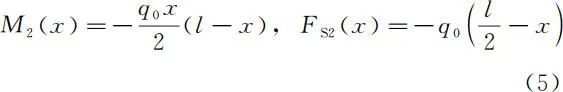
按照弹性力学来定义内力和杆端外力的正负号，就可以将材料力学中梁弯曲的基本公式以及挠曲线近似微分方程都统一起来。这样，对于图 1 和图 2 所示的坐标系，梁弯曲的基本公式和挠曲线近似微分方程如下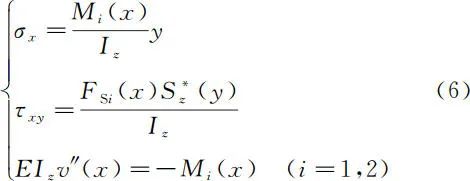于是，将式(4)代入式(6)中，即可得到图 1 坐标系下梁弯曲的正应力 σx 和切应力

。同样，将式(5)代入式(6)中，即可得到图 2 所示问题的正应力 σx 和切应力

。

通过对比可知：按照弹性力学与按照材料力学所定义的内力及杆端外力正负号，对于图 1 所示坐标系下的梁弯曲问题，两者完全相同；对于图 2 所示坐标系下的梁弯曲问题，两者关于切应力

不完全相同，它们相差一个负号，这是由于弹性力学与材料力学关于切应力的正负号规定不同所引起的。

进一步，我们可以给出图 1 和图 2 所示坐标系下梁弯曲问题的弹性力学正确解答。对于图 1 所示的梁弯曲问题，其弹性力学的正确解答为

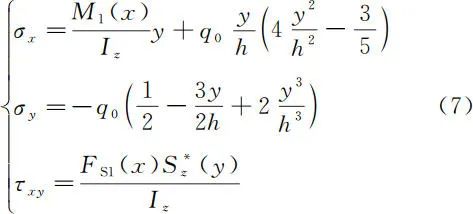对于图 2 所示的梁弯曲问题，其弹性力学的正确解答为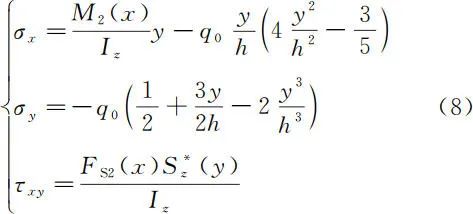可见，按照弹性力学来定义内力和杆端外力主矢量及主矩的正负号，就能保证弹性力学正确解答中完整地体现材料力学的基本解答，且在形式上具有一致性。顺便指出，如果按照材料力学来定义内力和杆端外力主矢量及主矩的正负号，对于图 2 所示的梁弯曲问题，其切应力

的弹性力学正确解答将与材料力学基本解答不完全相同，它们之间相差一个负号。

3 典型应用实例

3.1 平面问题圣维南原理中的应用

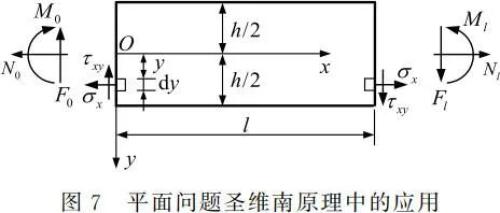
在应用圣维南原理时，需要将小边界上的精确应力边界条件（函数方程）替换为用主矢量和主矩表示的积分应力边界条件（代数方程）。当小边界面为坐标面时，直接利用静力等效方法来建立其积分的应力边界条件是十分方便的[5]。此时，在小边界上应用圣维南原理，可以直接地表述为：在同一小边界面上，应力的主矢量和主矩分别等于外力（面力）的主矢量和主矩[6]。例如，对于图 7 所示的平面问题，在小边界 x = 0 和 x = l 上，其积分的应力边界条件可以统一写为

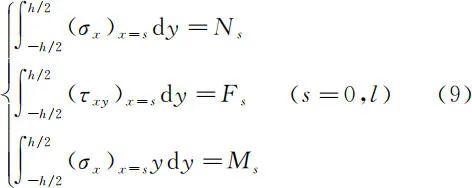
在实际的应用中，需要注意如下两点：

（1）在式(9)中，等号左边表示坐标面上应力的主矢量和主矩，右边表示外力（面力）的主矢量和主矩。其中，应力主矢量和主矩的正负号是直接由应力分量的正负号规定来确定的，即：正的应力分量方向，就是应力主矢量的正方向；正的应力分量乘以正的力臂，如 ( + σx ) × ( + y )，得出的力矩方向就是应力主矩的正方向。顺便指出，对于坐标面上 y < 0 的部位，其应力分量 σx 仍为正值，而力臂为负值，因此所合成主矩的方向仍与 y > 0 的部位转向一致。

（2）在式(9)中，Ns、Fs 及 Ms 仅表示外力主矢量和主矩的绝对值，而其方向在小边界面上均已按照正方向标出，如图 7 所示。若实际外力的主矢量和主矩方向与所标出的正方向不一致时，则只需在相应的主矢量或主矩绝对值前加负号即可。顺便指出，由于式(9)左边第三式中应力主矩是绕坐标原点的，外力的主矩也必须是同一点，因此需要事先将外力按照静力等效原则移置到坐标原点处。

3.2 变分解法中的应用

在弹性力学变分解法中，往往需要计算外力功，引入主矢量及主矩正负号的统一规定，可以直观、便捷地判断外力功的正负号。例如，图 8 所示坐标系下的等截面直梁，在梁的上表面作用有分布荷载 q(x)，在梁的端面上作用有适当的剪力和弯矩（均按正方向标出），使梁保持平衡，其中 v(x) 为梁轴线的挠度。现在，用梁的挠度 v(x) 来表示外力功，由于挠度 v(x) 与 y 轴正向一致时为正，转角以 x 轴正向转向 y 轴正向时为正，因此外荷载所做的功即为

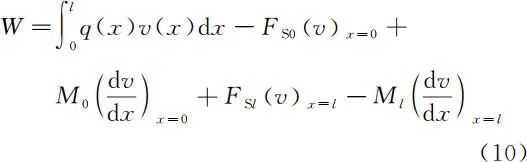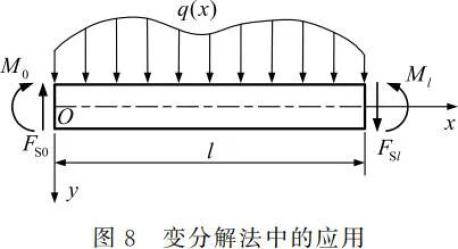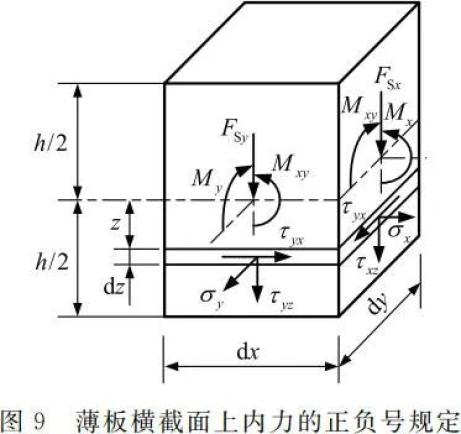
如果实际的外力方向与标出的正方向不一致时，只需在式(10)中将相应的外力加上负号即可。3.3 薄板弯曲问题中的应用

在薄板弯曲问题中，板边上的应力边界条件往往需要应用圣维南原理，建立由内力表示的静力边界条件，而且薄板是按内力来设计的，这就需要求出薄板横截面的内力。为此，按照弹性力学中内力主矢量和主矩的正负号统一规定，薄板弯曲问题中弯矩、扭矩和横向剪力的正负号规定即为：弯矩 Mx、My 分别使薄板横截面上 z > 0 的一侧产生正号的正应力 σx、σy 时为正；扭矩 Mxy、Myx 分别使薄板横截面上 z > 0 的一侧产生正号的切应力

、

时为正；横向剪力 FSx、FSy 分别使薄板横截面产生正号的切应力

、

时为正，如图 9 所示，其中薄板的中面为 xy 面，z 轴垂直向下。

对于薄板板边上的静力边界条件，以矩形薄板为例，板边中面上的总分布剪力、弯矩及角点集中力（反力）的正负号规定，如图 10 所示。需要说明的是，薄板板边上总分布剪力、弯矩的正负号分别与横截面上剪力、弯矩的正负号规定是一致的，而角点反力的正负号则取决于角点处扭矩的正负号，而不能再另行规定。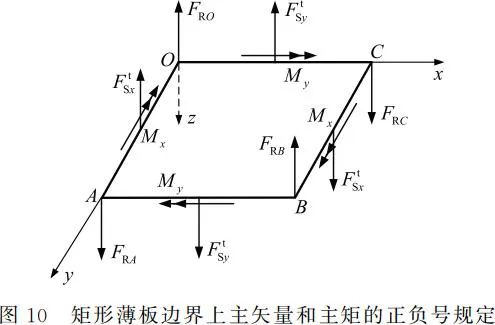3.4 空间问题圣维南原理中的应用

对于空间问题，在小边界上应用圣维南原理时，其积分的应力边界条件是 6 个。为了方便起见，假定在小边界上的外力已经事先按照静力等效原则移置到坐标原点处。例如，在图 11 所示的坐标系中，在小边界 z = 0 上作用有主矢量 Fx、Fy、Fz 和主矩 Mx、My、Mxy，应用圣维南原理建立积分的应力边界条件为

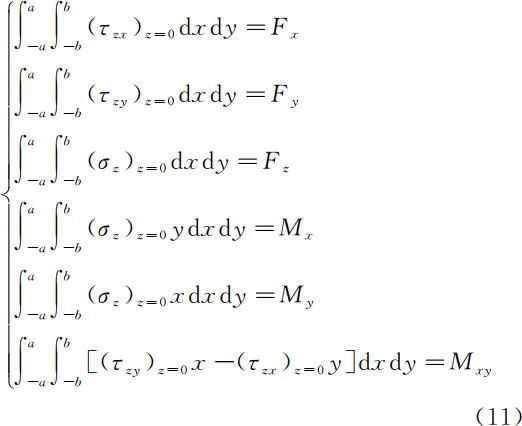
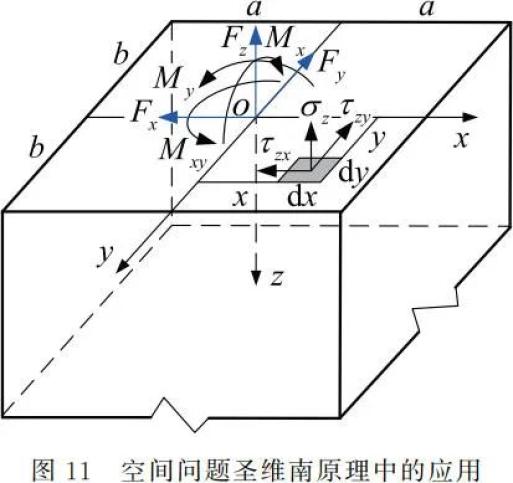需要指出的是，主矢量 Fx、Fy、Fz 分别是由边界上应力分量

、

、σz 的主矢量来静力等效，它们的正方向直接与相应的应力分量正方向相同；弯矩 Mx、My 分别是由应力分量 σz 绕 x 轴和 y 轴的主矩来静力等效，它们的正方向应当与 σz 绕 x 轴和 y 轴的转向相同。然而，扭矩 Mxy 是由应力分量

和

的主矩共同来静力等效的，由于

和

绕 z 轴的转向不一致，扭矩正方向就不能简单地由某个应力分量来直接确定，此时需要按照右手螺旋法则，以右手大拇指沿着边界面外法线方向为正，这样扭矩 Mxy 与

绕 z 轴的转向就为正，而应力分量

绕 z 轴的转向为负。这与薄板弯曲问题中的扭矩不同。

4 结语

本文通过深入剖析材料力学中内力主矢量及主矩的正负号规定，建议弹性力学中按应力分量来统一定义内力和外力的主矢量及主矩正负号，这不仅可以解决材料力学解答与弹性力学解题的一致性问题，而且还可以统一处理不同的弹性力学问题。教学实践表明，弹性力学中主矢量及主矩的正负号统一规定，概念清晰、便于理解，可以避免因定义不同而带来混淆，因坐标不同而产生差异，因问题不同而各自定义，使得学生在学习过程中对力学概念更加明晰，数学逻辑更加清晰，教学过程更加有效。

参考文献

[1]陈奎孚, 何坤娜. 力学分析中的正号与负号[J]. 物理与工程, 2017, 27(2): 15-21.

CHEN K F, HE K N. On the plus and minus signs in mechanics analysis [J]. Physics and Engineering, 2017, 27(2): 15-21. (in Chinese)

[2]孙训方, 方孝淑, 关来泰, 编, 胡增强, 郭力, 江晓禹, 修订. 材料力学（I）[M]. 5 版. 北京: 高等教育出版社, 2009.

[3]金忠谋. 材料力学（I）[M]. 2 版. 北京: 机械工业出版社, 2008.

[4]张爱军, 吴禄祥. “弹性力学”教学中几个难点问题的探讨[J]. 黑龙江教育（高教研究与评估）, 2019, (1): 13-15.

ZHANG A J, WU L X. Discussion on several difficult problems in the teaching of “Elasticity” [J]. Heilongjiang Education (Higher Education Research & Appraisal), 2019, (1): 13-15. (in Chinese)

[5]刘章军, 吴勃, 卢海林. 弹性力学与有限元基础[M]. 北京: 高等教育出版社, 2019.

[6]徐芝纶. 弹性力学简明教程[M]. 4 版. 北京: 高等教育出版社, 2013.

基金项目：2020 年湖北省高等学校省级教学研究项目（项目号：2020481），2020 年国家级一流本科课程《弹性力学 B》（证书号：2020131022），2020 年度“湖北名师工作室”主持人人才资助项目。

作者简介：刘章军，男，武汉工程大学教授，主要从事工程力学教学和工程结构抗灾可靠性研究，liuzhangjun73@aliyun.com。

引文格式: 刘章军, 阮鑫鑫. 弹性力学中主矢量及主矩正负号的统一表达[J]. 物理与工程, 2022, 32(5): 34-39.

Cite this article: LIU Z J, RUAN X X. Unified expression on the signs of principal vector and principal moment in elastic mechanics[J]. Physics and Engineering, 2022, 32(5): 34-39. (in Chinese)

END

更多精彩文章请点击下面“蓝字”标题查看：

对麦克斯韦方程组拓展的评论王青教授：深入理解“拓展的麦克斯韦方程组”——2.0版王青教授：理解王中林院士“拓展的麦克斯韦方程组”“碰瓷”麦克斯韦：伽利略协变和洛伦兹协变电磁场论趣谈热点：运动介质洛伦兹协变电磁理论2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授：源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感：教育中的现实和远方王青教授：昨晚（6月9日），清华电动力学期末考试朱邦芬院士：“减负”误区及我国科学教育面临的挑战《物理与工程》2022年第3期目录乐永康：新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡：对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士：从基础科学班到清华学堂物理班朱邦芬院士：对培养一流拔尖创新人才的思考李学潜教授：物理是一种文化李学潜教授：如何帮助物理系学生迈过从高三到大一这个坎穆良柱：物理课程思政教育的核心是科学认知能力培养穆良柱：什么是物理及物理文化？穆良柱：什么是ETA物理认知模型穆良柱：什么是ETA物理教学法吴国祯教授：我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写

陈佳洱，赵凯华，王殖东：面向21世纪，急待重建我国的工科物理教育王亚愚教授：清华物理系本科人才培养理念与实践葛惟昆教授：关于中外人才培养的几点思考安宇教授：为什么传统的课堂讲授模式需要改变安宇教授：其实教学就是积累的过程刘玉鑫教授：关于本科生物理基础课程教学和教材编著的一些思考沈乾若：重创理科教育的美加课程改革Henderson C：美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊，是中国科技核心期刊，1981年创刊，欢迎踊跃投稿，期刊投审稿采编平台：

http://gkwl.cbpt.cnki.net

欢迎关注

《物理与工程》微信公众号

原标题：《弹性力学中主矢量及主矩正负号的统一表达》

阅读原文