Nature Reviews Physics 综述：控制具有复杂节点的复杂网络

原创 D’Souza 等 集智俱乐部

导语

从互联网、人类社会网络到生物网络，真实世界的网络常包含数百万个异质节点。这些复杂网络不仅节点之间的连接模式复杂，单个节点也可能很复杂。要如何控制具有如此多复杂节点的复杂网络呢？今年3月发表于 Nature Reviews Physics 的综述文章“Controlling complex networks with complex nodes”指出，结合统计物理和控制理论可以为此提供新视角，架起微观节点和宏观网络的桥梁。该综述回顾了领域最新进展，并提供了一份研究指南。今天的文章是对综述文章的全文翻译。

关键词：复杂系统，复杂网络，统计物理，控制理论，机器学习

Raissa M. D’Souza, Mario di Bernardo & Yang-Yu Liu | 作者

朱欣怡 | 译者

胡一冰 | 审校

论文题目：

Controlling complex networks with complex nodes

论文地址：

https://www.nature.com/articles/s42254-023-00566-3

目录

摘要

1. 引言

2. 背景

3. 现有建模范式

4. 新范式和建模技术

5. 研究指南

摘要

真实世界的网络常含有数百万个异质节点，这些节点有跨时间尺度和空间尺度相互作用。为理解、建模和控制这些系统，统计物理（statistical physics）和控制理论（control theory）等领域都提供了不同的视角。这些领域之间更多的交互和新范式（如异质性和多层次表示）的集成，对解决现实系统来说是必要的。研究者们可以结合统计物理拓展模型、整合（正负）反馈的概念和拓展控制理论公式，从介观角度进行分析（mesoscopic analysis）以计算整体自由度的平均值。同时，还需要整合理论模型、机器学习和数据驱动等控制方法。本综述回顾了最新的进展，并发现了有助于理解和控制真实系统（从振荡器网络和社会网络到生物和技术网络）的新契机。

1. 引言

统计物理学主要关注节点集的平衡（equilibrium）和宏观系综性质，并为理解和预测大量简单和相同实体的集体行为提供了一个框架。这种行为的典型实例包括描述气体粒子的麦克斯韦-玻尔兹曼速度分布，还包括当材料被冷却到居里温度（Tc）时的铁磁相变。

相反，传统的控制理论逐渐演变为动力系统和工程的一个分支，致力于按照预期自动地控制系统或设备，使其能够忽略噪声、延迟和扰动。这涉及到设计反馈策略，在理想情况下希望通过影响相对较少的微观自由度，引导目标系统的动力学行为与期望演变同步。

然而现代网络规模巨大（如互联网或人类交互网络），人们无法完全了解每一个自由度及其相互联系，更不用说对所有自由度进行控制。因此，亟需架起宏观和微观的桥梁，建立平衡和动力学方法之间的联系，以控制具有复杂节点的复杂网络（complex networks with complex nodes）。本文强调“复杂”这一形容词，与复杂系统（complex systems）意义上的“复杂”相同，这意味着此系统是具有非线性行为的潜在异构系统。具体而言，“复杂网络”是指节点之间的连接模式，“复杂节点”是指单个节点有非线性行为。

本文的组织结构如下：

首先，介绍研究背景。具体包括（1）关于复杂网络和控制理论在统计物理的学科交叉点；（2）一般反馈控制理论和在真实网络应用中的挑战。

接着，介绍并讨论现有的方法与思想，主要为适用于指导和控制复杂网络行为的统计物理和控制理论。然后，文章提出了可能有效的新方法和建模技术。

最后，作者总结了一套研究指南，以促进未来跨学科发展。

在此明确贯穿全文的两个控制理论中的基本概念：可控性（controllability）和可观测性（observability）。

可控性是指控制输入的存在性，描述了人们在有限时间内通过合适的输入选择，引导动力系统从任何初始状态到任何期望的最终状态的能力。

可观测性是通过衡量系统的输入和输出来估计系统内部状态的能力，通常识别携带足够信息的变量子集来重构系统的行为。注意，文中使用术语“控制理论”来指代专注于分析和设计反馈系统以实现预期目标的工作主体。

2. 背景

2.1 统计物理与结构可控性

1990年代后期，随着互联网和万维网迅速发展、基因组数据和基础设施系统逐步完善、经济全球化势不可挡，网络科学[1]应运而生。统计物理的工具（如：随机图模型、生成函数和速率方程等）有助于人们更好地理解复杂网络的性质和行为——通常被描述为具有广泛规模、跨越几个数量级的潜在度分布。网络结构带来的关键影响是对随机干扰鲁棒、对针对攻击脆弱以及潜在的缺乏传染阈值。除了度分布，网络的显著结构特征包括小世界性、模块性和三元闭包[2]（图1）。

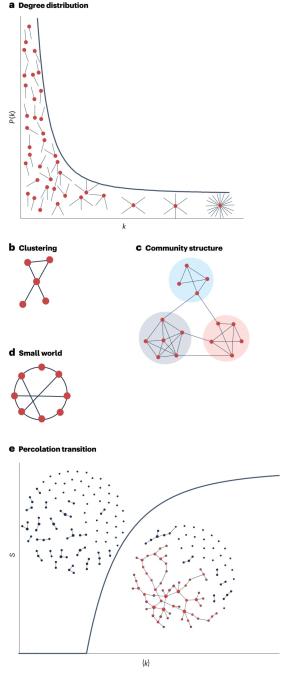
图1. 复杂网络中的常见指标。a.节点度（k）在较大尺度上的分布（P）；b.集聚系数；c.社区结构：节点可以被分配到组内的连接密度高于组之间的连接密度的组。d.小世界属性：大多数节点不直接相连，而是通过网络上的短路径链接。e.相变，例如渗流相变，其中网络的最大连通片大小S随着平均度的增加而表现出相变。

2011年，统计物理与复杂网络控制之间建立了重要联系，以分析研究具有线性动力学和任意度分布的网络系综（network ensemble）的可控性[3]。这种联系建立在结构控制的框架上，20世纪70年代的一篇文章[4]，通过图论方法解决了线性动力学网络上的可控性问题。问题在于，当应用在特定节点（[3]中的“驱动节点”(driver nodes)）时，如何确定是否存在控制输入能在有限时间内引导动力系统从任何初始状态到任何期望的最终状态，即使其可控。解决此问题的关键灵感来自于将识别最小驱动节点集的问题映射到网络上的最大匹配问题（图2），然后使用统计物理学的空腔方法（在“统计物理方法”一节中深入讨论）进行分析解决。

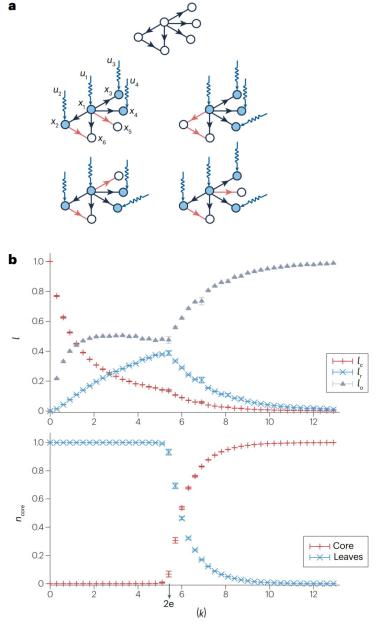
图2. 结构控制框架中的驱动节点的识别和相变。
a. 线性节点动力学（状态变量）有向网络上最大匹配问题的求解。能够识别最小驱动节点集，保证整个系统的结构可控性。对于一般有向网络（如图），可能有多个最大匹配（红色连边集）。因此，可以识别多个最小驱动节点集合（蓝色节点）。对于每个驱动器节点，必须施加确保结构可控性所必需的唯一控制信号（ui，蓝色波浪形箭头）。
b. 控制鲁棒性（robustness）和核心渗流（core percolation）。量化不可避免的边故障下控制的鲁棒性，可以通过计算连边l的类型：
1）临界（critical，lc），若其不存在，则必须增加驱动节点的数量以保持对系统的完全控制。换句话说，lc是网络的所有最大匹配的一部分。
2）冗余（redundant，lr），移除此类边不影响当前的驱动节点集。也就是说，它不属于任何最大匹配。
3）一般（ordinary，lo），既非关键，也不冗余。

lr作为平均度函数的非单调行为（上半部分）与网络中的核心渗流跃迁（下半部分）密切相关，其中ncore是核中节点的比例。当不同的最大匹配的数量开始呈指数增加时，发生核心渗流，这使得冗余连边的比例下降。

对于有向ER随机网络，核心渗流发生在平均度=2e时（下半部分）。图经许可改编自参考文献[3]。

在结构控制中，连边是否存在（即结构）比连边的权重更重要。传统上，结构控制框架假设节点根据线性非时变动力学演化：

（有关非线性动力学的详细信息和扩展，请参见“新范式和建模技术”一节）。这种线性意味着：可以用线性代数的工具来阐明网络结构和可控性之间的联系，包括网络结构中的相变连接[5，6]。此外，还建立了可控性转变和控制状态轨迹的非局部性和控制输入的非局部性之间的平衡。

除了结构控制之外，许多研究已经深入理解了控制能量（control energy）[8]、控制配置文件（control profiles）（基于控制流模式）[9]和来自现实世界系统的约束[10]。相关更全面的综述，请参见参考文献[11，12]。物理学家的控制理论综合入门，见参考文献13。然而，如何从统计物理的方法扩展到动态、非平衡、非线性的系统？这个问题仍然悬而未决。

2.2 控制理论综述

在经典的控制范式中，人们感测和控制感兴趣的特定系统或设备的行为，例如汽车、飞机或机器人。控制设计通常从感兴趣的系统的结构和动力学的数学（或计算）表示开始，并且包括合成反馈控制策略，该反馈控制策略通过感知系统行为来计算所需的输入以驱动系统达到期望的状态。负反馈提供了稳定行为的能力，即使在存在噪声、延迟或扰动的情况下，也具有保证鲁棒性的一些期望性能。相反，正反馈可以用于在非线性系统中实现双稳定性和分叉，驱动系统能达到多个稳定状态。

顺着控制策略的思想，已经发展了许多针对线性和非线性系统的数学公式[14]。这些方法中，许多是分布式或分散式的，并且有些使用了复杂的非线性、自适应、计算和时变方法[15]。多数方法集中在单个系统上，这意味着所有相关的自由度及其动力学和耦合都是已知的（图3a）。然而，这一经典范式面临着新兴应用的挑战——如何应用到大规模、通过复杂的网络关系相互作用的动力学系统中（图3b）。当下，控制这种复杂的网络来协调它们的集体行为是控制理论的核心问题和热门研究主题，最早可以追溯到Šiljak在20世纪70年代后期的开创性工作[16]。

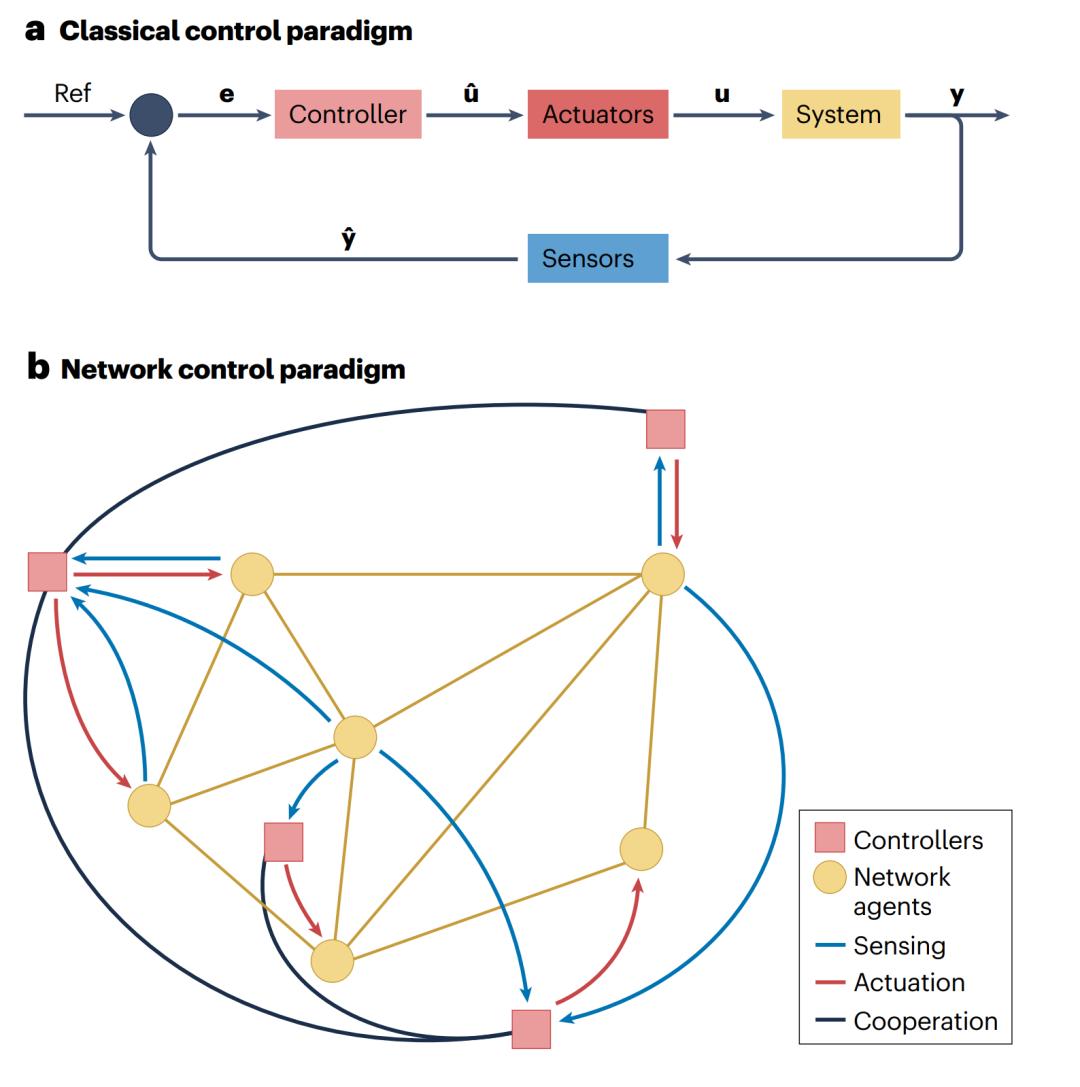
图3. 控制范式。
a）经典反馈控制范式。系统的控制输出y被传感器测量或估计；测量输出
反馈回比较节点（黑灰色），测量
和参考信号（Ref）的差；控制误差e被馈送到控制器，该控制器再根据某个控制规则计算控制输入（u1）；计算的输入通过一组驱动器在系统的实际输入（u）中实现；在这种情况下，所有相关的自由度及其耦合都是已知的。
b）分布式分散牵制控制策略。一些网络节点（黄色圆圈）向控制器（粉色方块）发送包含其状态或输出的信息（蓝色箭头）。控制器合作（黑边）制定网络控制策略，然后选择性地干预网络中部分节点（红色箭头）的行为，以实现一些期望的集体行为。
图片由Davide Salzano提供。

从控制的角度来看，复杂网络是由许多连续时间或离散时间单元组成的大规模动态系统的例子，这些个体可以通过静态或时变的互连网络进行交互[16,17]。

因为需要在我们感兴趣的宏观行为（如共识或同步）与微观行动之间建立反馈联系，以设计所需的集体动力学机制，所以关键问题就成了

1.判断给定网络是否满足基本的控制属性（例如可控性和可观测性）；

2.如何在不同尺度上闭合反馈回路（图4）？

实现控制的方法有：控制网络节点、赋予边动力学属性、通讯协定（communication protocol）、控制网络本身的结构或组合以上方法。一个突出的例子是牵制控制（pinning control）[18 -21]，其中只需控制相对小部分的网络节点或边缘就能够控制系统的集体行为朝一些参考平衡或渐近轨迹[22，23]发展。然而，我们还想要设计策略控制更一般的、有更广泛节点动力学的系统（如，网络结构随时间或是节点动力学函数演变）。

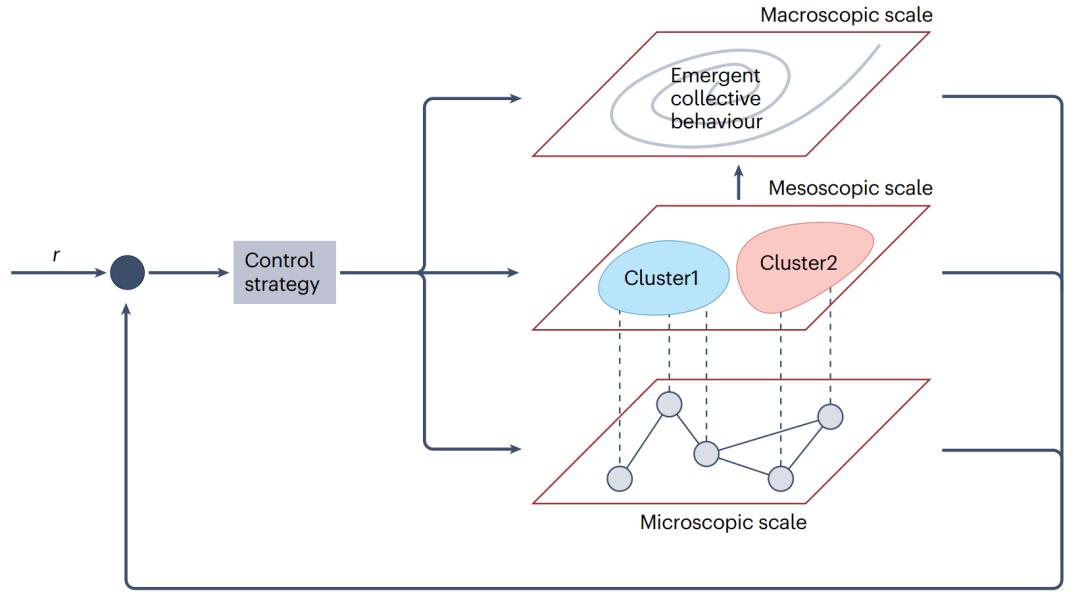
图4. 复杂网络中的闭合反馈回路需要在不同尺度上进行感测、计算和驱动（actuation）。感测和制动可以在图中描绘的任何尺度下执行。在该图中，为了简单起见，我们描绘了集中式控制策略；然而，当处理网络系统时，控制策略通常是分布式和分散式的。注意r是表示系统的期望行为的参考信号。图片由Marco Coraggio提供。

2.3 复杂网络背景下的控制

交叉学科真实世界网络对控制主要提出了三点挑战：

一、可能存在多个长度尺度和时间尺度的行为和交互，包括个体之间会相互影响的自组织行为。在某些情况下，我们只关注集体行为（例如，感染总人数）。然而在其他情况下，我们有可能对微观细节感兴趣（例如，哪些特定的人被感染）。同样地，对于测量和输入控制信号与自由度相互作用的能力，可能存在约束。此外，有时我们或许不需要非得将系统控制到特定状态，只需要简单地控制，使系统远离不期望的状态（例如系统崩溃）或朝向期望状态可能就足够了。参考文献[10，24，25]中有对真实系统的干预中的高维性，非线性和约束所带来的挑战的深入讨论。

二、网络本身具有模糊性。在大脑网络中，节点可以是单个神经元、神经元块、甚或是跨越大量神经元的脑区。研究节点之间的交互，学习连接模式（如“线路图，wiring diagram”）此类的实验成本很高，并且无法学习到完整的连接模式。注意，单个边的存在与否对介数中心性之类的属性有明显的影响。此外，网络上发生的动力学活动与拓扑结构同样重要。例如，在交通网络中，确定拥堵模式的是网络流和网络拓扑。长程序就这样从节点动力学和网络结构的相互作用中涌现而出[26，27]。

三、将异质性（heterogeneity）和多尺度结合起来意味着，系统的不同部分可能需要不同类型的表征。其中一些能够用离散时间动力学建模，而另一些可能需要基于连续时间；某些方面可能需要用常微分方程（ODE）描述，另一些方面则需要用偏微分方程（PDE）描述。例如，在交通管理应用中，ODE能很好地描述车流的运动；而PDE在描述个体级别的车辆接受信号灯或其他信号的建模中，更具优势。如何整合这种分析仍然悬而未决，还有噪音和不确定性在旁“蠢蠢欲动”。最后，此应用领域的跨度也很大，从电网到社会网络到生物系统，各自有不同的目标和约束，这就意味着我们必须谨慎地选择一个恰当的建模范式。

建模时的关键问题是：

1.我们测量什么？

2.什么因素有影响？

3.何时影响？

4.如何影响？

此外，研究如何收敛到目标状态与保持复杂网络控制策略鲁棒性和弹性的恰当方法也至关重要。

3. 现有建模范式

3.1 统计物理方法

统计物理学的概念和技术已广泛用于研究复杂网络的结构和动力学特性[2，28，29]，研究领域覆盖网络生长（network growth），相变和级联故障（cascading failures）等复杂网络基本行为。从统计物理学的角度研究控制这些行为并不是为了严格满足可控属性，更像是在控制系统：例如，引导它远离临界点或减少故障发生。直接应用统计物理工具来研究复杂网络的传统控制性质主要涉及到可控性和可观测性。我们将在接下来讨论这些主题，并将方法总结在表1中。

表1. 基于统计物理的概念和方法，用于研究复杂网络的结构、动力学或控制特性

为了研究复杂网络的生长，特别是以幂律分布而闻名的无标度网络[30]，已经有了许多具有强烈统计物理色彩的分析方法，例如连续统理论[31]、主方程方法[32]和速率方程方法[33]。

统计物理学的一个核心研究点是相变（临界点外部控制参数的小扰动，使系统宏观行为发生剧烈变化的现象）[34]。在网络的背景下，有一个著名的相变，就是渗流相变（图1e），可以使用随机图模型进行分析[35]。这些模型基于统计系综的概念，是统计物理学的基础。

网络的统计系综考虑给定的一组属性，例如指定的度分布。系综中的每个体系是具有特定节点和连边构型的网络实现，并有其出现的概率（即，统计权重）。除了给定的属性集之外，我们假设其他属性都是完全随机的，因此它们可以通过使用一些平均场方法在整个系综上平均，例如基于分支过程和树假设的生成函数形式[36，37]。

渗流相变描述了网络中大规模连通片的突现，逐渐连通过程中的小扰动可以控制临界点的位置，并可能导致爆炸性渗流[38，39]。对于临界转变，已有研究表明，系统到达临界点时，预测的涨落和自相关时间会增加，这可以作为早期的预警信号[40，41]。

统计物理学中自组织研究的理论基础是自组织临界性（self-organized criticality, SOC）的范式[42]。在SOC中，竞争力的平衡（例如驱动和耗散）会导致系统接近临界点，从而引发遵循幂律分布的级联故障。这种级联故障在复杂网络（如电网和脑网络）中时有发生[43]。通过驱动力的性质来控制SOC是统计物理学文献中的一个重要主题[44 -47]，正如最近“龙王”事件[48 -51]备受关注（‘dragon king’ events，灾难转变前兆）。

统计物理工具在可控性和可观测性方面的直接应用是存在的。下面，我们将介绍几个完全从网络结构（或连接模式）的角度，研究控制特性的典型案例。

其一是应用空腔法（cavity method）来解决结构控制问题[3]。由于结构可控性定理[4]的图形解释，人们可以简单地检查网络结构，来检查网络结构是否可控，而避免依赖复杂的边权矩阵运算。特别地，我们可以识别动力节点（driver nodes）的最小集合，其时间相关控制（time-dependent control）足以控制系统的整个动力学。这种识别可以通过将结构控制问题映射成为最大匹配的纯图论问题来实现[52 -54]。利用统计物理学的空腔方法[55 -57]（及其在解决最大匹配问题[58]中的进一步应用），可以分析计算具有指定度分布的网络系综的某些控制属性[3]。这些属性包括：最大匹配的大小，它与确保结构可控性的驱动器节点（或控制输入）的最小数目直接相关；以及不同最大匹配的总数，它与不同控制配置的数量直接相关，并且会因此影响控制鲁棒性。

另一典例是电网的可观测性研究。在该系统中，可以使用相量测量单元（phasor measurement units，PMU）来确定节点的电压（还可看作状态变量）。PMU能够测量其对应节点的实时电压和线路电流，因此PMU不仅能确定其所放置的节点的状态变量，还能确定其所有最近邻居的状态变量。在这种情况下，可观测性问题可以映射成一个纯粹的图论问题。事实上，PMU的随机放置会导致网络可观测性转换[59]，可以使用母函数形式（generating function formalism）进行分析研究[36，37]。此外，识别电网中传感器节点（即PMU）的最小集合问题可以映射成为经典的图论问题：尽管它通常求解困难，但最小支配集问题可以通过消息传递算法（源于自旋玻璃理论）来解决，该算法提供了接近最优的解决方案，并且在真实网络中表现良好[60]。

如何将控制问题映射为纯图论问题？任何控制属性（如控制能量成本），都需要相关领域的具体知识，而且纯粹的图论解释和相应的统计集成方法在此无用武之地。随机矩阵理论[61]中可以直接处理复杂网络边权重的技术，这对适当的网络系综的建模来说必不可少。一般来说，具体的结构和动力学都很重要[62]。

3.2 控制理论方法

传统控制理论方法的目的是分析和操纵特定系统的行为。控制问题可以概括成如下三个：确定需要感测什么、需要控制什么以及如何用感测信息实现控制目标。因此，任何控制设计的三个关键要素是感测、计算和驱动[14]。表2中总结了一些方法。

表2. 控制理论中用于分析和控制复杂网络的概念和方法。

多智能体系统中经典控制目标包含一致性（consensus，即所有单元会朝着同一个平衡点收敛）[63-71]和同步性（synchronization，即收敛到渐进时变解[asymptotic time-varying solution]）[72-75]，同时也还包括如编队控制（formation control）[76 -78]，模式生成（pattern formation）[79]和多智能体协同运动（如集群）[80]等目标。控制目标通常根据性能（侧重于瞬态特性，例如建立时间、上升时间和超调量）、稳定性（例如收敛到状态空间中的平衡或流形）以及对噪声和外部扰动的鲁棒性来制定[14]。

从系统的数学（或数据驱动）模型和控制目标出发，我们可以尝试：1.建立系统的可控性和可观测性；2.设计控制策略，并通过对闭环网络系统中的这些特性进行适当的严格证明，证明该控制策略能保证所需行为的收敛性和稳定性（图5）。

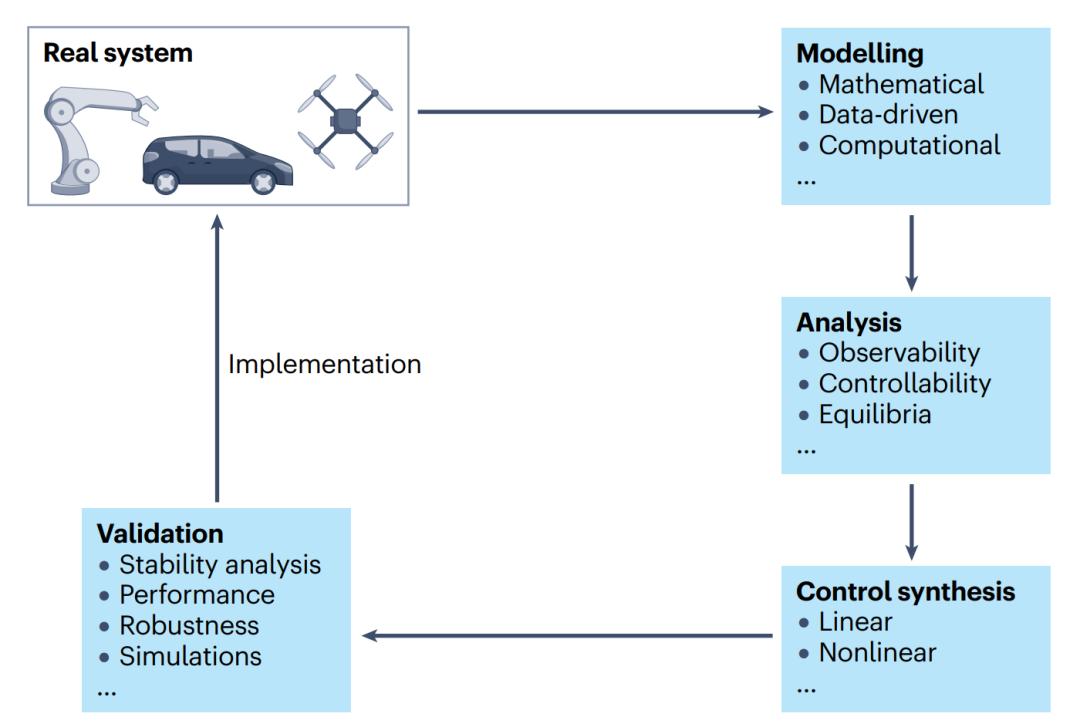
图5. 经典闭环控制器设计的主要阶段。始于真实系统，先建模分析其在没有控制的情况下的性质。然后设计控制策略以满足目标要求，须在实施之前进行验证。通常，这种设计方法在实现精确的控制之前需要多次迭代。丨图像来源：Gian Carlo Maffettone

我们常希望设计分布式和分散式策略来处理多智能体系统，不必以集中的方式决定感测、制动和控制输入。某些控制问题也用无需反馈的开环策略来解决，但一旦存在扰动，稳定性和性能要求就无法被满足，就不够鲁棒。因此在此处，我们只关注闭环反馈控制策略。

可控性问题是一个存在性问题，关注在给定网络结构、主体的动力学和连边交互的情况下，引导集体行为需要控制哪些节点。在复杂网络的背景下，无法通过秩来判断是否系统是否能控时，可以使用结构可控性的和Gramians可控性来解决这个问题[81-85]。尽管过去十年可控性问题取得了显著进展，但仍然存在许多未决的问题，包括理解非线性或时变系统网络中的可控性，或者当网络结构随时间或动力学函数（状态依赖网络演化）演化时的可控性。

研究可观测性问题是为了发现哪些变量的信息量足以重现整个系统行为。当应用于大规模复杂网络时，可观测性的评估也变得复杂繁琐，因为它取决于能重塑整体网络动力学的变量。同样，控制的方法（如结构可观性理论）也是为了这一目的[82，86-88]。然而现在仍有许多可观测性问题有待解决（如研究非线性动力系统的时变网络结构的可观测性）。

由于图论工具可以补充和增强代数或几何基础理论，复杂网络的可控性和可观测性方法与传统的控制理论方法相比有明显变化。这一重要研究方向在20世纪70年代末由Šiljak的早期工作[16]中首次得到承认，并在后来的工作中得到进一步发展[82]，它使得处理大量相互作用的动态变量具有可行性。（我们注意到，使用图论方法来研究网络问题至少可以追溯到20世纪60年代的数学社会学社群。[89]）

如果已经分析了目标系统的基本特性，就可以设计反馈控制策略（闭环策略）了。通过观测信息和控制输入，来操纵系统以实现控制目标。验证控制策略的一个基本问题是分析和证明受控网络系统从不同的初始条件（稳定性）和外部扰动（鲁棒性）下的收敛性。通过借鉴同类系统的稳定性和鲁棒性方法，现已推广出许多研究动力系统复杂网络稳定性和鲁棒性的方法。（关于可用方法，详见参考文献[17，21-23，90-95]）。

关于稳定性，研究给定复杂网络系统的局部或全局稳定性的方法包括两方面：

1.将网络系统视为一个整体，研究其在扰动下的稳定性的方法；

2.研究节点以某种方式耦合时，系统保持稳定的方法。

考虑整个网络系统的分析工具包括：基于李亚普诺夫直接法的方法[90]或基于线性化工具（如主稳定性函数方法，master stability function）的方法[96]。其他的有效方法包括增量稳定性和使用收敛工具，如收缩理论[23,92-95]或增量被动性[91]。这些理论工具也适用于研究连接稳定性[16]相关概念的其他问题，譬如前面提到的另一个核心问题——底层网络结构如何影响发生在其上的动力学。

控制设计的方法在文献中比比皆是，各领域基于动态优化控制理论的控制设计方法包括：最优控制、博弈理论、自适应控制、智能控制、非线性控制、模型预测控制和鲁棒控制等等。目前，基于机器学习的数据驱动方法和控制策略也越来越多地被用于控制复杂网络的行为。更多信息详见参考文献[97，98]，在“新范例和建模技术”一节中，我们也有讨论。

尽管在控制理论的研究领域有许多进展，但仍有许多挑战有待解决。最近控制学界致力于研究噪声对网络中系统集体行为的影响、抗扰动能力（包括结构扰动）、发展协同和共识策略以保障节点的隐私，以及网络系统中扰动传播分析与控制[99-109]。

3.3 动力系统方法

正如统计物理学对控制策略的启发，动力系统方法也打开了控制策略的思路。控制策略常旨在操纵和影响系统，而不是严格的可控。有许多方法直接利用系统的非线性性质，还有利用数据驱动的方法（如系统识别）。我们接下来将聊聊这些内容。

给定动力学方程对系统的行为及其吸引子、极限环和吸引盆边界的相空间进行建模，可以找到利用自然轨迹将系统驱动到相空间的期望区域的蓄意扰动（strategic perturbations）。早期，这一领域的控制混沌的后续工作[111 -113]证明了这种可能性是混沌吸引子[110]。最近，学者们已解决了如何通过一系列考虑了扰动约束的策略性反冲来实现控制[114]。虽然利用相空间中的自然轨迹看上去完美，但在实践中它难以提供传统控制理论所必需的严格性能保障和对噪声的鲁棒性。例如，吸引盆的边界可以是网状的或分形的。

在相关文献中，有大量关于嵌合体状态（chimaera states）控制的工作[115]。嵌合体状态由对称耦合的相同振荡器系统中相干和非相干动力学的共存所定义，故显示出惊人的对称破缺性质[116、117]。这方面的研究包括延时反馈控制[118 -120]、牵制控制[121]、周期性强迫[122]、通过拓扑结构控制[123]或耦合修改[124]以及多层网络中嵌合体的控制[125]。参考文献[126]以自组织非线性动力系统为中心进行了综述，虽然还有许多方向有待探索。

通常，系统的运动方程是未知的，甚至连状态空间也可能是未知的。但是系统上的数据可能很丰富。如果一个系统上的数据，即可观测量，是它状态的函数，人们就可以从时间序列数据中推断出系统的演化。例如，许多文献中有用于系统识别或网络推断的技术（如文献[127-129]及其参考文献）。在下一节中，我们将讨论基于算子理论和稀疏识别技术的最新方法。

4. 新范式和建模技术

本节讨论如何改进前述方法，使之更适合真实系统。

4.1 网络复杂性会增加多少？

近年来，增加网络复杂性一直是物理学研究的焦点。“网络”在形式上由元素之间的成对交互的集合组成，但是真实网络中经常可以找到超越二元的高阶交互作用。例如，在化学反应网络中，反应进行可能需要三种试剂；在共同作者网络中，常有多个作者。有人用超图（hypergraphs）和单纯复形（simplicial complexes）来解决这个挑战[130，131]。该部分前沿进展包括定义统计系综[132，133]、分析可接受的同步模式、完全同步[134 -136]和集群同步[137，138]的稳定性以及可控性[139]，但目前特定问题的控制（ad hoc control）策略尚未完全开发。

同样，提供网络动力学的瞬时描述[140-141]的活动驱动时序网络（activity-driven temporal networks）的范式也富有成效。在这种方法中，每个节点的活动潜力（activity potential）是根据该节点相对活动程度来确定的，相对活动程度可以从给定时间窗的时序网络数据集中测出，活动电位分布函数可以表征系统级动力学。

真实世界系统通常是多层网络（multilayered networks）形式的。例如，每个人有许多种社会身份，关键基础设施网络通常具有物理分层或逻辑分层结构。这一概念是多层网络结构控制（structural control of multiplex networks）[142、143]、使用图论捕捉分层关键基础架构[144、145]和使用多重控制策略[146]的基础。

4.2 人们能控制非平衡统计物理模型吗？

统计物理学方法倾向于关注平衡系统，但对于细致平衡（detailed balance，严格热动平衡）的系统仍存在涨落耗散关系（fluctuation–dissipation relations）。例如，可以使用双量子点模型（double quantum dot model）[147]上的反馈控制方案将热量转换为功，这一发现正推动关于反馈控制和涨落的进一步研究[148]。同样，有几个经典的驱动远离平衡系统的模型，如自组织临界性[42]（在“统计物理方法”一节有叙述）、Kardar-Parisi-Zhang（KPZ）方程[149]和不对称简单排斥过程（ASEP）模型[150]。尽管这些模型伴随着许多普遍现象（由一般属性支配，一般属性独立于系统的动力学细节的基本对称性），但我们仍可以用反馈来影响和控制行为。

4.3 结构控制框架较线性模型好多少？

结构控制的经典框架中有一个基本限制：基于线性非时变动力学。

其中A,B中的元素都是零或独立的自由参数。这个框架基于线性系统的结构可控性的概念。如果我们说系统（A,B）是结构可控的，那就是说，可以在A,B中设置特定非零元素，使得系统可控。这需要满足卡夫曼可控性判据（Kalman’s criterion of controllability）：

最近，有学者在结构控制框架的基础上提出了非线性系统结构可达性（structural accessibility）的概念[151-152]，并将其适用于一般非线性系统：

动力学假设的条件不严，要求f(x(t))和g(x(t))是亚纯函数（meromorphic functions）。亚纯函数一词源于希腊语 (meros)，定义为两个整函数之比，只有有限阶、孤立的极点和零点，无非必要奇点。结构可达性的概念可以被认为是线性系统中结构可控性的非线性推广。令人惊讶的是，结构可达性和结构可控性几乎有相同的图论条件。二者关键区别是，“自循环”（对应内禀节点动力学）是结构可控性的图论充分条件，而非结构可达性的充分条件。这种结构可达性框架可以从底层网络结构中识别驱动节点[151]，并已在生态和生化系统中得到了应用。

4.4 如何处理大型复杂的多智能体系统？

另一个紧迫的众所周知的控制难题是，如何解决复杂系统的动力学的节点数目限制？或者更准确地说，让系统出现涌现行为时节点数目仍保持不变。在这种情况下，问题就变成了：找到一个对目标可观测量（我们希望控制的）的宏观描述。这样做需要目标变量在宏观尺度和被控微观个体层面的闭循环。对于极其复杂和大型的网络，即使是线性时变的系统，都很难实现除了识别驱动节点之外的任何控制目标。

连续化（continuification or continuation）方法[153，154]将由大量常微分方程描述的微观问题，转化为描述宏观水平上目标可观测量的偏微分方程（PDE）（连续化阶段）。然后，使用控制偏微分方程[155、156]的技术来设计宏观控制动作，并且最终将所得的控制律离散化，使得其可以被部署回到微观个体级别[157]。在这种方法中，挑战就转变成了寻找连续化目标问题然后离散化的方法，在微观水平上进行分布式控制策略。然而主要障碍是当从PDE得到的控制律被离散化时，大多数微观个体通常会受到控制输入的影响，这与牵制控制的思想（控制少的节点实现目标）相反。

另一个框架是基于线性系统的大规模网络的图子控制（graphon control）[158]。图子（graphon）是收敛图序列的极限，形成了一种自然的非参数方法来建模和估计超大型网络[159]。由于其与统计物理、极值组合学和网络上的非参数统计分析的联系被广泛讨论[160 -162]，图子理论（Graphon theory）已经成为图论的一个子领域。

基于图子的控制复杂大型网络系统的策略由三个步骤组成：

一、当节点数趋于无穷大时，首先确定有限网络系统序列S的图子极限。

二、在此约束下解决相应的控制问题。

三、通过逼近极限系统的控制律，生成沿着有限网络系统的序列S的任何系统的控制律。

该策略已被用于大规模复杂网络的状态控制问题和线性二次型调节器问题。

图子博弈（graphon games）的概念源于网络博弈和干预的统计框架。此框架是用图子理论研究大型网络干预的另一典例。但如何利用图子理论来控制具有一般非线性动力学的任意大网络仍有待解决。

随着研究渐渐开始面向更大规模的网络，通过控制和观察介观尺度来控制目标复杂网络的问题变得愈发重要，这样的介观尺度可以是群体或节点或连边的集群水平。这个方向有待进一步研究，并且需要从控制的观点来定义适当的介观层次。

4.5 我们能用数据重构运动方程吗？

除了成熟的系统识别（system identification）方法之外，还有其他的方法可以重建有效的运动方程。

Koopman算子方法就是其中一种。它是对可观测向量空间的线性变换，用著名的Koopman算子的特征函数将其表示为线性展开式，以实现从无限维的观测空间到线性的演化。不稳定性与具有正本征值的模式有关，甚至可以通过相关联的本征向量中的相对振幅来识别各个节点在不稳定性中的作用。Koopman算子用于动力系统分析的能力已经毋庸置疑[164，165]，并且也可以应用于非线性流[166]中，例如近期在应用最优控制器[167，168]和反馈控制[169 -171]的方法中效果显著。参考文献[172]是一本实用的入门书，参考文献[173，174]介绍了最近的两个综合应用。

另一种不同的数据驱动方法依赖于这样的假设——尽管数据是高维的，但动力学主要只受几个主要变量的影响，使得方程在可能的函数空间中是稀疏的。稀疏性促进技术和机器学习可以在有噪声的测量数据上组合使用以识别控制方程，这是一种被称为非线性动力学的稀疏识别（sparse identification of nonlinear dynamics，SINDY）[175]的技术。SINDY已被扩展到包括驱动的影响，并且能显示如何基于有限的噪声数据增强模型预测控制的性能[176]。

我们常用降维技术将高维时间序列数据映射到低维子空间，然后用非线性动力学的稀疏识别（SINDY）来确定失去的动力学信息。

如果所得到的相空间由几个固定点组成，我们就可以调节系统，诱导期望的不稳定性和吸引子，从而实现高维、非线性、网络系统的前馈控制[177]。

4.6 如何使用机器学习和数据驱动的控制方法来征服复杂性？

随着计算能力的提高，应用中有趣的复杂性问题越来越多，基于机器学习和数据驱动方法的复杂网络控制方法在各科技领域变得越来越普遍。

典型的例子包括互联自动驾驶车辆的原型设计。Google Waymo (https://waymo.com) 等公司已经提出使用深度学习设计自动驾驶汽车或实现自动车辆排队的方法，如卡车排队。（https://highways.dot.gov/research/laboratories/saxton-transportation-operations-laboratory/Truck-Platooning）

还有在自主机器人和群体机器人领域中，机器学习的计算技术[178]使用频率也愈加频繁。如前所述，已经有很多在不同场景下对网络进行数据驱动控制的方法，但是我们仍然没有在更普适的环境中使用这些方法的框架。

然而，当问题太难分析解决时，数据驱动和机器学习方法[179，180]可能是唯一的选择，例如当无法推导出数学模型或要解决的任务太复杂时。当目标是通过在时间上动力学自适应来实现控制时，其时序网络的结构会响应动力学的变化，从而各节点的状态依此进行交互[140、141]（参见参考文献[181]以获得更简单的说明性示例）。考虑到实际应用中的目标通常是，在存在故障或扰动的情况下，赋予网络重塑其结构的能力以保持其所需的功能，因此解决这个问题在实际应用中极为重要。例如，自组织电网能够自我隔离以防止故障或电流过载、自动驾驶车辆或机器人组能改变其互连结构以更好地执行避障或复杂机动的情况。

5. 研究指南

要想推进前沿和解决实际问题，就需要推进多学科和交叉学科的研究。不仅要征服复杂性，还要顺势利用它，来实现更好的控制性能、来解决更复杂的问题。研究目标应该是双重的：

第一，要弥补学科之间差距，将平均场方法等技术的使用扩展到复杂网络的控制中去[182]。同时，要考虑到现实的约束条件和实现反馈策略的需要，以保证研究问题所需的稳定性、目标性能和鲁棒性。

第二，确定一组范例问题或标准案例用于验证和对比控制复杂系统的不同方法。这样做非常重要，因为在许多不同领域中出现的应用程序和在特定领域中开发的技术可以被抽象以解决更一般的问题。例如分析非线性振荡器（如神经元）的动力学相位响应曲线技术，最近就有人利用它来实现更普遍类别的非线性系统的控制（见参考文献[183]和其中的参考文献）。

为了推动这一领域的发展并促进跨学科的合作，我们需要集体共同努力。为解决控制复杂系统的基本问题，第一个呼吁就是：发起一系列针对标准方法的挑战！在计算机科学领域，举行挑战赛已经成为一种传统。目前已经有一系列成功的挑战赛，如微软想象杯、谷歌人工智能挑战赛、ImageNet挑战赛和Netflix奖等等。可以说，这些挑战（如ImageNet挑战）促进了当今的人工智能的繁荣。同样地，在系统生物学和医学领域，也有一个很好的挑战赛榜样，即梦想挑战赛（DREAM challenges）。该比赛提供高质量的生物医学标准数据集，邀请参与者针对指定问题提出解决方案，促进交流并在此过程中建立合作团体。网络控制领域的研究人员也可以从其他领域现有的挑战平台中学习，以进一步推进领域前沿，让“群众的智慧”发挥对出最大的科学效益。

由于控制复杂系统具有多学科性质，挑战不必集中在纯理论问题上，也可以是应用甚至是转化。例如，有人试图对定向人类蛋白质相互作用网络进行结构可控性分析，以鉴定疾病基因和药物靶点[184]，虽然这方面的研究还有待进一步深入。此外，为了设计更好地操纵人类肠道微生物组的方法，控制理论也能有许多潜在的应用（人类内部生态系统由数万亿微生物组成，相互作用方式很复杂）[185]。譬如，在该领域中一个非常实际的控制问题是设计明确定义的活聚生体组（consortium of live microorganisms）（通常叫做益生菌混合物、细菌，即药物或活生物治疗产品）以防止某些病原体寄身，从而预防感染[186]。此外，标准测试方法（benchmarking methods）还可以用于保护和控制微型电网（microgrids，即具有确定电边界的本地电网，充当单个和可控的实体）[187]。

总之，我们的最终目标是将来自不同科学技术领域的工具和技术结合起来，解决在不同尺度上闭合控制回路的关键问题，从而协调大规模复杂系统的集体行为，这将会对大量交叉学科的应用产生极大影响。

参考文献

National Research Council. Network Science (The National Academies Press, 2005).

Newman, M. E. J. Networks: An Introduction (Oxford Univ. Press, 2018).

Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Controllability of complex networks. Nature 473,

167–173 (2011).

Lin, C.-T. Structural controllability. IEEE Trans. Autom. Control. 19, 201 (1974).

Liu, Y. Y., Csoka, E., Zhou, H. & Posfai, M. Core percolation on complex networks.

Phys. Rev. Lett. 109, 205703 (2012).

Jia, T. et al. Emergence of bimodality in controlling complex networks. Nat. Commun. 4,

2002 (2013).

Sun, J. & Motter, A. E. Controllability transition and nonlocality in network control.

Phys. Rev. Lett. 110, 208701 (2013).

Yan, G., Ren, J., Lai, Y.-C., Lai, C.-H. & Li, B. Controlling complex networks — how much

energy is needed? Phys. Rev. Lett. 108, 218703 (2012).

Ruths, J. & Ruths, D. Control profiles of complex networks. Science 343, 1373–1376

(2014).

Motter, A. E. Networkcontrology. Chaos 25, 097621 (2015).

Liu, Y.-Y. & Barabási, A.-L. Control principles of complex systems. Rev. Mod. Phys. 88,

053006 (2016).

Xiang, L., Chen, F., Ren, W. & Chen, G. Advances in network controllability. IEEE Circuits

Syst. Mag. 19, 8–32 (2019).

Bechhoefer, J. Control Theory for Physicists (Cambridge Univ. Press, 2021).

Åström, K. J. & Murray, R. M. Feedback Systems: An Introduction for Scientists and

Engineers 2nd edn (Princeton Univ. Press, 2021).

Khalil, H. K. Nonlinear Systems (Prentice Hall, 2002).

Siljak, D. D. Large-scale Dynamic Systems: Stability and Structure (North-Holland, 1978).

Bullo, F. Lectures on Network Systems 1.6 edn (Kindle Direct Publishing, 2022).

Li, X., Wang, X. & Chen, G. Pinning a complex dynamical network to its equilibrium.

IEEE Trans. Circuits Syst. 51, 2074–2087 (2004).

Wang, X. & Chen, G. Pinning control of scale-free dynamical networks. Phys. A Stat.

Mech. Appl. 310, 521–531 (2002).

Sorrentino, F., di Bernardo, M., Garofalo, F. & Chen, G. Controllability of complex

networks via pinning. Phys. Rev. E 75, 046103 (2007).

Su, H. & Wang, X. Pinning Control of Complex Networked Systems 1st edn (Springer, 2013).

Moreau, L. Stability of multiagent systems with time-dependent communication links.

IEEE Trans. Autom. Control 50, 169–182 (2005).

Cisneros-Velarde, P., Jafarpour, S. & Bullo, F. Contraction theory for dynamical systems on

Hilbert spaces. IEEE Trans. Autom. Control 67, 6710–6715 (2021).

Murray, R. M. Control in an Information Rich World (Society for Industrial and Applied

Mathematics, 2003).

Lamnabhi-Lagarrigue, F. et al. Systems and control for the future of humanity, research

agenda: current and future roles, impact and grand challenges. Annu. Rev. Control 43,

1–64 (2017).

Matheny Matthew, H. et al. Exotic states in a simple network of nanoelectromechanical

oscillators. Science 363, eaav7932 (2019).

Salova, A. & D’Souza, R. M. Decoupled synchronized states in networks of linearly

coupled limit cycle oscillators. Phys. Rev. Res. 2, 043261 (2020).

Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys.

74, 47–97 (2002).

Dorogovtsev, S. N., Goltsev, A. V. & Mendes, J. F. F. Critical phenomena in complex

networks. Rev. Mod. Phys. 80, 1275 (2008).

Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286,

509–512 (1999).

Albert, R. & Barabási, A.-L. Topology of evolving networks: local events and universality.

Phys. Rev. Lett. 85, 5234–5237 (2000).

Dorogovtsev, S. N., Mendes, J. F. F. & Samukhin, A. N. Structure of growing networks with

preferential linking. Phys. Rev. Lett. 85, 4633–4636 (2000).

Krapivsky, P. L., Redner, S. & Leyvraz, F. Connectivity of growing random networks.

Phys. Rev. Lett. 85, 4629–4632 (2000).

Stanley, H. E. Introduction to Phase Transitions and Critical Phenomena (Oxford Univ.

Press, 1971).

Erdős, P. & Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hungarian

Acad. Sci. 5, 17–61 (1960).

Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Random graphs with arbitrary degree

distributions and their applications. Phys. Rev. E 64, 026118 (2001).

Callaway, D. S., Newman, M. E. J., Strogatz, S. H. & Watts, D. J. Network robustness and

fragility: percolation on random graphs. Phys. Rev. Lett. 85, 5468–5471 (2000).

Achlioptas, D., D’Souza, R. M. & Spencer, J. Explosive percolation in random networks.

Science 323, 1453–1455 (2009).

D’Souza, R. M., Gómez-Gardeñes, J., Nagler, J. & Arenas, A. Explosive phenomena in

complex networks. Adv. Phys. 68, 123–223 (2019).

Scheffer, M. et al. Early-warning signals for critical transitions. Nature 461, 53–59 (2009).

Boettiger, C. & Hastings, A. Quantifying limits to detection of early warning for critical

transitions. J. R. Soc. Interface 9, 2527–2539 (2012).

Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality: an explanation of the 1/f noise.

Phys. Rev. Lett. 59, 381–384 (1987).

D’Souza, R. M. Curtailing cascading failures. Science 358, 860–861 (2017).

Cajueiro, D. O. & Andrade, R. F. Controlling self-organized criticality in sandpile models.

Phys. Rev. E 81, 015102 (2010).

Cajueiro, D. O. & Andrade, R. F. Dynamical programming approach for controlling the

directed Abelian Dhar–Ramaswamy model. Phys. Rev. E 82, 031108 (2010).

Noël, P.-A., Brummitt, C. D. & D’Souza, R. M. Controlling self-organizing dynamics on

networks using models that self-organize. Phys. Rev. Lett. 111, 078701 (2013).

Qi, J. & Pfenninger, S. Controlling the self-organizing dynamics in a sandpile model on

complex networks by failure tolerance. EPL 111, 38006 (2015).

Sornette, D. Dragon-kings, black swans and the prediction of crises. CCSS Working

Paper No. CCSS-09-005 (2009).

Cavalcante, H. L., Oria, M., Sornette, D., Ott, E. & Gauthier, D. J. Predictability and

suppression of extreme events in a chaotic system. Phys. Rev. Lett. 111, 198701 (2013).

Lin, Y., Burghardt, K., Rohden, M., Noël, P.-A. & D’Souza, R. M. Self-organization of dragon

king failures. Phys. Rev. E 98, 022127 (2018).

Mikaberidze, G. & D’Souza, R. M. Sandpile cascades on oscillator networks: the BTW

model meets Kuramoto. Chaos 32, 053121 (2022).

Yamada, T. & Foulds, L. R. A graph-theoretic approach to investigate structural and

qualitative properties of systems: a survey. Networks 20, 427 (1990).

Commault, C., Dion, J. M. & Van Der Woude, J. W. Characterization of generic

properties of linear structured systems for efficient computations. Kybernetika 38,

503–520 (2002).

Murota, K. Matrices and Matroids for Systems Analysis (Springer, 2009).

Mézard, M. & Parisi, G. The Bethe lattice spin glass revisited. Eur. Phys. J. B 20, 217 (2001)

Mézard, M. & Parisi, G. The cavity method at zero temperature. J. Stat. Phys. https://doi.org/

10.1023/A:1022221005097 (2003).

Mezard, M., Parisi, G. & Virasoro, M. Spin Glass Theory and Beyond Vol. 9 (World Scientific,

1986).

Zdeborová, L. & Mézard, M. The number of matchings in random graphs. J. Stat. Mech.

Theory Exp. 05, P05003 (2006).

Yang, Y., Wang, J. & Motter, A. Network observability transitions. Phys. Rev. Lett. 109,

258701 (2012).

Zhao, J.-H, Habibulla, Y. & Zhou, H.-J. Statistical mechanics of the minimum dominating

set problem. J. Stat. Phys. 159, 1154–1174 (2015).

Wigner, E. P. Random matrices in physics. SIAM Rev. 9, 1–23 (1967).

Gates, A. J. & Rocha, L. M. Control of complex networks requires both structure and

dynamics. Sci. Rep. 6, 24456 (2016).

Olfati-Saber, R. & Murray, R. M. Consensus problems in networks of agents with switching

topology and time-delays. IEEE Trans. Autom. Control. 49, 1520–1533 (2004).

Paley, D. A., Leonard, N. E., Sepulchre, R., Grunbaum, D. & Parrish, J. K. Oscillator models

and collective motion. IEEE Control. Syst. Mag. 27, 89–105 (2007).

Jadbabaie, A., Lin, J. & Morse, A. S. Coordination of groups of mobile autonomous agents

using nearest neighbor rules. IEEE Trans. Autom. Control. 48, 988–1001 (2003).

Tanner, H. G., Jadbabaie, A. & Pappas, G. J. Flocking in fixed and switching networks.

IEEE Trans. Autom. Control. 52, 863–868 (2007).

Leonard, N. E. & Fiorelli, E. Proc. 40th IEEE Conference on Decision and Control

(Cat. No.01CH37228) (IEEE, 2001).

Olfati-Saber, R. Flocking for multi-agent dynamic systems: algorithms and theory.

IEEE Trans. Autom. Control 51, 401–420 (2006).

Olfati-Saber, R., Fax, J. A. & Murray, R. M. Consensus and cooperation in networked

multi-agent systems. Proc. IEEE 95, 215–233 (2007).

Wei, R. & Beard, R. W. Consensus seeking in multiagent systems under dynamically

changing interaction topologies. IEEE Trans. Autom. Control 50, 655–661 (2005).

Sepulchre, R. Consensus on nonlinear spaces. Annu. Rev. Control 35, 56–64 (2011).

DeLellis, P., diBernardo, M. & Garofalo, F. Novel decentralized adaptive strategies for the

synchronization of complex networks. Automatica 45, 1312–1318 (2009).

Dorfler, F., Chertkov, M. & Bullo, F. Synchronization in complex oscillator networks and

smart grids. Proc. Natl Acad. Sci. USA 110, 2005–2010 (2013).

Scardovi, L. & Sepulchre, R. 2008 47th IEEE Conference on Decision and Control 546–551

(IEEE, 2008).

Wieland, P., Sepulchre, R. & Allgöwer, F. An internal model principle is necessary and

sufficient for linear output synchronization. Automatica 47, 1068–1074 (2011).

Andrea, R. D. & Dullerud, G. E. Distributed control design for spatially interconnected

systems. IEEE Trans. Autom. Control 48, 1478–1495 (2003).

Bullo, F., Cortés, J. & Martínez, S. Distributed Control of Robotic Networks: A Mathematical

Approach to Motion Coordination Algorithms (Princeton Univ. Press, 2009).

Shamma, J. S. (ed.) Cooperative Control of Distributed Multi-agent Systems (John Wiley

& Sons, Ltd, 2007).

Oh, K.-K., Park, M.-C. & Ahn, H.-S. A survey of multi-agent formation control. Automatica

53, 424–440 (2015).

Kumar, V., Leonard, N. & Morse, A. S. Cooperative Control (Springer Berlin, 2005).

Porfiri, M. & di Bernardo, M. Criteria for global pinning-controllability of complex

networks. Automatica 44, 3100–3106 (2008).

Mesbahi, M. & Egerstedt, M. Graph Theoretic Methods in Multiagent Networks (Princeton

Univ. Press, 2010).

Mesbahi, M. On state-dependent dynamic graphs and their controllability properties.

IEEE Trans. Autom. Control 50, 387–392 (2005).

Rahmani, A., Ji, M., Mesbahi, M. & Egerstedt, M. Controllability of multi-agent systems

from a graph-theoretic perspective. SIAM J. Control Optim. 48, 162–186 (2009).

Pasqualetti, F., Zampieri, S. & Bullo, F. Controllability metrics, limitations and algorithms

for complex networks. IEEE Trans. Control Netw. Syst. 1, 40–52 (2014).

Bianchin, G., Frasca, P., Gasparri, A. & Pasqualetti, F. The observability radius of networks.

IEEE Trans. Autom. Control 62, 3006–3013 (2017).

Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Observability of complex systems. Proc. Natl Acad.

Sci. USA 110, 2460–2465 (2013).

Sundaram, S. & Hadjicostis, C. N. Structural controllability and observability of linear

systems over finite fields with applications to multi-agent systems. IEEE Trans. Autom.

Control 58, 60–73 (2013).

Harary, F., Norman, R. Z. & Cartwright, D. Structural Models: An Introduction to the Theory

of Directed Graphs (John Wiley & Sons, 1965).

Xiang, J. & Chen, G. On the V-stability of complex dynamical networks. Automatica 43,

1049–1057 (2007).

Arcak, M. Passivity as a design tool for group coordination. IEEE Trans. Autom. Control 52,

1380–1390 (2007).

Slotine, J.-J. E. & Wang, W. in Cooperative Control: A Post-Workshop Volume 2003 Block

Island Workshop on Cooperative Control (eds Kumar, V., Leonard, N. & Morse, A. S.)

207–228 (Springer, 2005).

Forni, F. & Sepulchre, R. A differential Lyapunov framework for contraction analysis.

IEEE Trans. Autom. Control 59, 614–628 (2014).

Moylan, P. & Hill, D. Stability criteria for large-scale systems. IEEE Trans. Autom. Control

23, 143–149 (1978).

di Bernardo, M., Fiore, D., Russo, G. & Scafuti, F. in Complex Systems and Networks: Dynamics,

Controls and Applications (eds Lü, J., Yu, X., Chen, G. & Yu, W.) 313–339 (Springer, 2016).

Pecora, L. M. & Carroll, T. L. Master stability functions for synchronized coupled systems.

Phys. Rev. Lett. 80, 2109–2112 (1998).

Baggio, G., Bassett, D. S. & Pasqualetti, F. Data-driven control of complex networks.

Nat. Commun. 12, 1429 (2021).

Nguyen, T. T., Nguyen, N. D. & Nahavandi, S. Deep reinforcement learning for multiagent

systems: a review of challenges, solutions, and applications. IEEE Trans. Cybern. 50,

3826–3839 (2020).

Battistelli, G. & Chisci, L. Kullback–Leibler average, consensus on probability densities,

and distributed state estimation with guaranteed stability. Automatica 50, 707–718

(2014).

Dibaji, S. M., Ishii, H. & Tempo, R. Resilient randomized quantized consensus. IEEE Trans.

Autom. Control 63, 2508–2522 (2018).

Fiore, D. & Russo, G. Resilient consensus for multi-agent systems subject to differential

privacy requirements. Automatica 106, 18–26 (2019).

Nozari, E., Tallapragada, P. & Cortés, J. Differentially private distributed convex optimization

via functional perturbation. IEEE Trans. Control Netw. Syst. 5, 395–408 (2018).

Mo, Y. & Murray, R. M. Privacy preserving average consensus. IEEE Trans. Autom. Control

62, 753–765 (2017).

Xie, S., Russo, G. & Middleton, R. H. Scalability in nonlinear network systems affected by

delays and disturbances. IEEE Trans. Control Netw. Syst. 8, 1128–1138 (2021).

Stüdli, S., Seron, M. M. & Middleton, R. H. From vehicular platoons to general networked

systems: string stability and related concepts. Annu. Rev. Control 44, 157–172 (2017).

Russo, G., Wirth, F. & Shorten, R. On synchronization in continuous-time networks of

nonlinear nodes with state-dependent and degenerate noise diffusion. IEEE Trans.

Autom. Control 64, 389–395 (2019).

Li, T., Wu, F. & Zhang, J. Multi-agent consensus with relative-state-dependent

measurement noises. IEEE Trans. Autom. Control 59, 2463–2468 (2014).

Burbano-L, D. A., Russo, G. & Bernardo, M. D. Pinning controllability of complex network

systems with noise. IEEE Trans. Control Netw. Syst. 6, 874–883 (2019).

Della Rossa, F. & De Lellis, P. Synchronization and pinning control of stochastic coevolving

networks. Annu. Rev. Control 53, 147–160 (2022).

Ott, E., Grebogi, C. & Yorke, J. A. Controlling chaos. Phys. Rev. Lett. 64, 1196–1199 (1990).

Ditto, W. L., Rauseo, S. N. & Spano, M. L. Experimental control of chaos. Phys. Rev. Lett.

65, 3211–3214 (1990).

Shinbrot, T., Grebogi, C., Ott, E. & Yorke, J. A. Using small perturbations to control chaos.

Nature 363, 411 (1993).

Boccaletti, S., Grebogi, C., Lai, Y.-C., Mancini, H. & Maza, D. The control of chaos: theory

and applications. Phys. Rep. 329, 103–197 (2000).

Cornelius, S. P., Kath, W. L. & Motter, A. E. Realistic control of network dynamics.

Nat. Commun. 4, 1942 (2013).

Bick, C. & Martens, E. A. Controlling chimeras. New J. Phys. 17, 033030 (2015).

Kuramoto, Y. & Davaasambuu, B. Coexistence of coherence and incoherence in nonlocally

coupled phase oscillators. Nonlin. Phenom. Complex Syst. 5, 380–385 (2002).

Abrams, D. M. & Strogatz, S. H. Chimera states for coupled oscillators. Phys. Rev. Lett. 93,

174102 (2004).

Sieber, J., Omel’chenko, O. E. & Wolfrum, M. Controlling unstable chaos: stabilizing

chimera states by feedback. Phys. Rev. Lett. 112, 054102 (2014).

Gjurchinovski, A., Scholl, E. & Zakharova, A. Control of amplitude chimeras by time delay

in oscillator networks. Phys. Rev. E 95, 042218 (2017).

Zakharova, A., Semenova, N., Anishchenko, V. & Schöll, E. Time-delayed feedback control

of coherence resonance chimeras. Chaos 27, 114320 (2017).

Gambuzza, L. V. & Frasca, M. Pinning control of chimera states. Phys. Rev. E 94, 022306

(2016).

Semenov, V., Zakharova, A., Maistrenko, Y. & Schöll, E. Delayed-feedback chimera states:

forced multiclusters and stochastic resonance. EPL 115, 10005 (2016).

Bera, B. K., Majhi, S., Ghosh, D. & Perc, M. Chimera states: effects of different coupling

topologies. EPL 118, 10001 (2017).

Ruzzene, G., Omelchenko, I., Schöll, E., Zakharova, A. & Andrzejak, R. G. Controlling

chimera states via minimal coupling modification. Chaos 29, 051103 (2019).

Omelchenko, I., Hülser, T., Zakharova, A. & Schöll, E. Control of chimera states in multilayer

networks. Front. Appl. Math. Stat. 4, 00067 (2019).

Schöll, E., Klapp, S. H. L. & Hövel, P. Control of Self-organizing Nonlinear Systems

(Springer, 2016).

Ljung, L. System Identification: Theory for User (Prentice Hall, 1999).

Xue, Y. & Bogdan, P. Reconstructing missing complex networks against adversarial

interventions. Nat. Commun. 10, 1738 (2019).

Timme, M. Revealing network connectivity from response dynamics. Phys. Rev. Lett. 98,

224101 (2007).

Battiston, F. et al. The physics of higher-order interactions in complex systems. Nat. Phys.

17, 1093–1098 (2021).

Bianconi, G. Higher-Order Networks (Cambridge Univ. Press, 2021).

Ghoshal, G., Zlatic, V., Caldarelli, G. & Newman, M. E. Random hypergraphs and their

applications. Phys. Rev. E 79, 066118 (2009).

Courtney, O. T. & Bianconi, G. Generalized network structures: the configuration model

and the canonical ensemble of simplicial complexes. Phys. Rev. E 93, 062311 (2016).

Lucas, M., Cencetti, G. & Battiston, F. Multiorder Laplacian for synchronization in

higher-order networks. Phys. Rev. Res. 2, 033410 (2020).

Gambuzza, L. V. et al. Stability of synchronization in simplicial complexes. Nat. Commun.

12, 1255 (2021).

Ferraz de Arruda, G., Tizzani, M. & Moreno, Y. Phase transitions and stability of dynamical

processes on hypergraphs. Commun. Phys. 4, 24 (2021).

Zhang, Y., Latora, V. & Motter, A. E. Unified treatment of synchronization patterns

in generalized networks with higher-order, multilayer, and temporal interactions.

Commun. Phys. 4, 195 (2021).

Salova, A. & D’Souza, R. M. Cluster synchronization on hypergraphs. Preprint at https://

doi.org/10.48550/arXiv.2101.05464 (2021).

Chen, C., Surana, A., Bloch, A. M. & Rajapakse, I. Controllability of hypergraphs.

IEEE Trans. Netw. Sci. Eng. 8, 1646–1657 (2021).

Perra, N., Goncalves, B., Pastor-Satorras, R. & Vespignani, A. Activity driven modeling

of time varying networks. Sci. Rep. 2, 469 (2012).

Liu, S., Perra, N., Karsai, M. & Vespignani, A. Controlling contagion processes in activity

driven networks. Phys. Rev. Lett. 112, 118702 (2014).

Posfai, M., Gao, J., Cornelius, S. P., Barabasi, A. L. & D’Souza, R. M. Controllability

of multiplex, multi-time-scale networks. Phys. Rev. E 94, 032316 (2016).

Menichetti, G., Dall’Asta, L. & Bianconi, G. Control of multilayer networks. Sci. Rep. 6,

20706 (2016).

González, A. D., Chapman, A., Dueñas-Osorio, L., Mesbahi, M. & D’Souza, R. M. Efficient

infrastructure restoration strategies using the recovery operator. Comput.-Aided Civ.

Infrastruct. Eng. 32, 991–1006 (2017).

Chapman, A., González, A. D., Mesbahi, M., Dueñas-Osorio, L. & D’Souza, R. M. 2017 IEEE

56th Annual Conference on Decision and Control (CDC) 493–498 (IEEE, 2017).

Burbano, D. & di Bernardo, M. Multiplex PI control for consensus in networks of

heterogeneous linear agents. Automatica 67, 310–320 (2016).

Annby-Andersson, B., Samuelsson, P., Maisi, V. F. & Potts, P. P. Maxwell’s demon in a

double quantum dot with continuous charge detection. Phys. Rev. B 101, 165404 (2020).

Bhattacharyya, D. & Jarzynski, C. From a feedback-controlled demon to an information

ratchet in a double quantum dot. Phys. Rev. E 106, 064101 (2022).

Kardar, M., Parisi, G. & Zhang, Y. C. Dynamic scaling of growing interfaces. Phys. Rev. Lett.

56, 889–892 (1986).

Spitzer, F. Interaction of Markov processes. Adv. Math. 5, 246–290 (1970).

Angulo, M. T., Moog, C. H. & Liu, Y.-Y. A theoretical framework for controlling complex

microbial communities. Nat. Commun. 10, 1045 (2019).

Angulo, M. T., Aparicio, A. & Moog, C. H. Structural accessibility and structural observability

of nonlinear networked systems. IEEE Trans. Netw. Sci. Eng. 7, 1656–1666 (2020).

Nikitin, D., Wit, C. C. D. & Frasca, P. A continuation method for large-scale modeling and

control: from ODEs to PDE, a round trip. IEEE Trans. Autom. Control 67, 5118–5133 (2021).

Nikitin, D. Scalable Large-scale Control of Network Aggregates (Université Grenoble

Alpes, 2021).

Krstic, M. & Smyshlyaev, A. Boundary Control of PDEs (SIAM Press, 2008).

Smyshlyaev, A. & Krstic, M. Adaptive Control of Parabolic PDEs (Princeton Univ. Press,

2010).

Maffettone, G., Boldini, A., di Bernardo, M. & Porfiri, M. Continuification control of

large-scale multiagent systems in a ring. IEEE Control Syst. Lett. 7, 841–846 (2023).

Gao, S. & Caines, P. E. Graphon control of large-scale networks of linear systems.

IEEE Trans. Autom. Control 65, 4090–4105 (2020).

Borgs, C. & Chayes, J. Proceedings of the 2017 ACM Conference on Economics and

Computation 665–672 (Association for Computing Machinery, 2017).

Lovász, L. Large Networks and Graph Limits Vol. 60 (American Mathematical Society, 2012).

Borgs, C., Chayes, J. T., Lovász, L., Sós, V. T. & Vesztergombi, K. Convergent sequences

of dense graphs I: subgraph frequencies, metric properties and testing. Adv. Math. 219,

1801–1851 (2008).

Lovász, L. & Szegedy, B. Limits of dense graph sequences. J. Comb. Theory Ser. B 96,

933–957 (2006).

Parise, F. & Ozdaglar, A. Graphon games: a statistical framework for network games and

interventions. Econometrica 91, 191–225 (2023).

Mezić, I. & Banaszuk, A. Comparison of systems with complex behavior. Phys. D Nonlin.

Phenom. 197, 101–133 (2004).

Mezić, I. Spectral properties of dynamical systems, model reduction and decompositions.

Nonlin. Dyn. 41, 309–325 (2005).

Rowley, C. W., MeziĆ, I., Bagheri, S., Schlatter, P. & Henningson, D. S. Spectral analysis

of nonlinear flows. J. Fluid Mech. 641, 115–127 (2009).

Brunton, S. L., Brunton, B. W., Proctor, J. L. & Kutz, J. N. Koopman invariant subspaces and

finite linear representations of nonlinear dynamical systems for control. PLoS ONE 11,

e0150171 (2016).

Kaiser, E., Kutz, J. N. & Brunton, S. L. Data-driven discovery of Koopman eigenfunctions

for control. Mach. Learn. Sci. Technol. 2, 035023 (2021).

Arbabi, H., Korda, M. & Mezić, I. 2018 IEEE Conference on Decision and Control (CDC)

6409–6414 (IEEE, 2018).

Peitz, S. Controlling nonlinear PDEs using low-dimensional bilinear approximations

obtained from data. Preprint at https://doi.org/10.48550/arXiv.1801.06419 (2018).

Peitz, S. & Klus, S. Koopman operator-based model reduction for switched-system

control of PDEs. Automatica 106, 184–191 (2019).

Arbabi, H. Koopman Spectral Analysis and Study of Mixing in Incompressible Flows. PhD

thesis, University of California (2017).

Brunton, S. L., Budišić, M., Kaiser, E. & Kutz, J. N. Modern Koopman theory for dynamical

systems. SIAM Rev. 64, 229–340 (2022).

Mauroy, A., Mezić, I. & Susuki, Y. The Koopman Operator in Systems and Control (Springer,

2020).

Brunton, S. L., Proctor, J. L. & Kutz, J. N. Discovering governing equations from data by

sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113,

3932–3937 (2016).

Kaiser, E., Kutz, J. N. & Brunton, S. L. Sparse identification of nonlinear dynamics for model

predictive control in the low-data limit. Proc. R. Soc. A Math. Phys. Eng. Sci. 474, 0335 (2018).

Morrison, M. & Kutz, J. N. Nonlinear control of networked dynamical systems. IEEE Trans.

Netw. Sci. Eng. 8, 174–189 (2021).

Hüttenrauch, M., Šošić, A. & Neumann, G. Deep reinforcement learning for swarm

systems. J. Mach. Learn. Res. 20, 1966–1996 (2019).

Garrabé, É. & Russo, G. Probabilistic design of optimal sequential decision-making

algorithms in learning and control. Annu. Rev. Control. 54, 81–102 (2022).

Hewing, L., Wabersich, K. P., Menner, M. & Zeilinger, M. N. Learning-based model

predictive control: toward safe learning in control. Annu. Rev. Control Robot. Auton. Syst.

3, 269–296 (2020).

Kempton, L. C., Herrmann, G. & di Bernardo, M. Distributed optimisation and control of

graph Laplacian eigenvalues for robust consensus via an adaptive multilayer strategy.

Int. J. Robust. Nonlin. Control 27, 1499–1525 (2017).

Fornasier, M. & Solombrino, F. Mean-field optimal control. ESAIM: COCV 20, 1123–1152

(2014).

Sepulchre, R. Spiking control systems. Proc. IEEE 110, 577–589 (2022).

Vinayagam, A. et al. Controllability analysis of the directed human protein interaction

network identifies disease genes and drug targets. Proc. Natl Acad. Sci. USA 113,

4976–4981 (2016).

Gilbert, J. A. et al. Current understanding of the human microbiome. Nat. Med. 24,

392–400 (2018).

Xiao, Y., Angulo, M. T., Lao, S., Weiss, S. T. & Liu, Y.-Y. An ecological framework to

understand the efficacy of fecal microbiota transplantation. Nat. Commun. 11, 3329

(2020).

Altin, N. & Eyimaya, S. E. 2021 10th International Conference on Renewable Energy

Research and Application (ICRERA) 412–417 (IEEE, 2021).

Watts, D. J. A simple model of global cascades on random networks. Proc. Natl Acad.

Sci. USA 99, 5766–5771 (2002).

Arcak, M., Meissen, C. & Packard, A. Networks of Dissipative Systems: Compositional

Certification of Stability, Performance, and Safety (Springer, 2016).

Bullo, F. Contraction Theory for Dynamical Systems 1.0 edn (Kindle Direct Publishing, 2022).

Lohmiller, W. & Slotine, J.-J. E. On contraction analysis for nonlinear systems. Automatica

34, 683–696 (1998).

Marden, J. R. & Shamma, J. S. Game theory and control. Annu. Rev. Control Robot.

Auton. Syst. 1, 105–134 (2018).

Lewis, F. L., Zhang, H., Hengster-Movric, K. & Das, A. Cooperative Control of Multi-Agent

Systems (Springer, 2014).

Gadjov, D. & Pavel, L. A passivity-based approach to nash equilibrium seeking over

networks. IEEE Trans. Autom. Control 64, 1077–1092 (2019).

Semsar-Kazerooni, E. & Khorasani, K. Multi-agent team cooperation: a game theory

approach. Automatica 45, 2205–2213 (2009).

Gharesifard, B. & Cortés, J. Distributed convergence to Nash equilibria in two-network

zero-sum games. Automatica 49, 1683–1692 (2013).

原标题：《Nature Reviews Physics 综述：控制具有复杂节点的复杂网络》

阅读原文