人造飞船逃逸地球三种方法的理论分析与数值模拟

原创 金惠吉 陈超 等 物理与工程

摘要

本文从三种逃逸地球的方法——“单次点火逃逸、两次点火逃逸（Oberth 效应）、三次点火逃逸（Edelbaum 效应）”出发，研究讨论了三种逃逸方式在喷气变轨时消耗燃料的多少以及飞船运行时间的计算方法，并根据理论进行了 VPyhton 数值模拟，模拟出的飞船三种逃逸方式和理论上的情况一致，最后又根据理论进行了 GeoGebra 作图定量分析比较了三种逃逸方式在燃料消耗以及运行时间上的大小关系。

关键词 飞船变轨；Oberth 效应；Edelbaum 效应；第二宇宙速度；VPython；GeoGebra；数值模拟

Abstract In this paper, the calculation methods of the fuel energy consumed by the three escape methods during the orbit change and the flight time of the spacecraft are discussed based on three escape methods: single ignition escape, double ignition escape (Oberth effect) and triple ignition escape (Edelbaum effect).VPyhton numerical simulation was carried out according to the theory, and the simulated three escape modes of the spacecraft were consistent with the theoretical situation. Finally, GeoGebra mapping was carried out according to the theory to quantitatively analyze and compare the relationship between the three escape modes in energy consumption and running time.

一般地，要让人造飞船从圆轨道逃逸地球，通过一次的点火加速即可。然而，在 1928 年，Hermann Oberth 提出了一种两次点火逃逸的方法，该方案可以更加节省燃料[1]，后来该方案又得到了更加详细的分析[2-3]，且在 1959 年又由 Theodore Edelbaum 进一步提出了一种三次点火逃逸的方案[4]。本文将对三种逃逸方案进行理论上的分析，并通过 VPython 对三种逃逸方案进行数值模拟，根据理论所模拟出的运行情况与理论分析一致，从而验证理论的正确性。接着又通过理论分析结合 GeoGebra 软件绘图比较在给定到达无穷远的速度大小的情况下三种逃逸策略最终所消耗的燃料情况，最后又比较了三种逃逸策略在到达给定的离地球的距离 r 时三者所用时间的关系，得出了四个关于耗燃料量以及航行时间的结论：(1)当到达无穷远时的速度 vw 接近于 0 时，单次逃逸最省燃料，三次点火逃逸次之；(2)当到达无穷远时的速度 vw 较大时，三次点火逃逸最省燃料，两次点火逃逸次之；(3)当 vw 较小且飞船到天体中心距离 r 较小时，单次逃逸所需时间最短，两次点火逃逸用时次之，但当 r 较大时，两次点火逃逸用时短；(4)当 vw 较大且在 r 一定时单次点火逃逸用时短，两次点火逃逸次之。

1 理论分析

1.1 飞船在椭圆轨道运行公式的导出

因飞船在椭圆轨道上运动过程种机械能守恒，以无穷远处为零势能点，有

设飞船到达无穷远处时速度大小达到最终速度 vw，在距离 r 处则为 vr，有

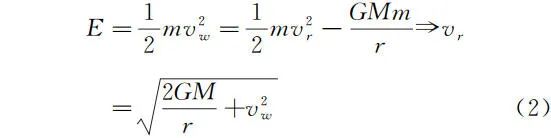
如图 1 所示，由角动量守恒，有

rAvA = rBvB (3)

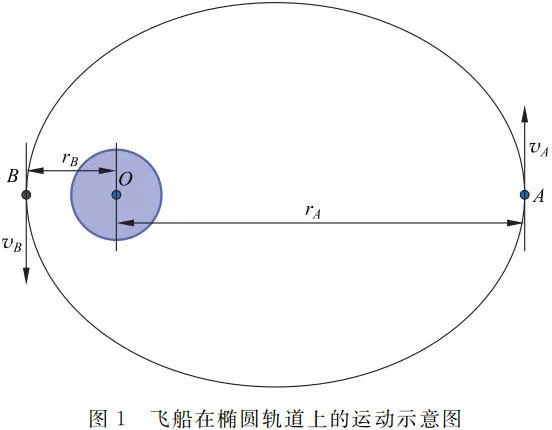
联立式（1）和式（3）得

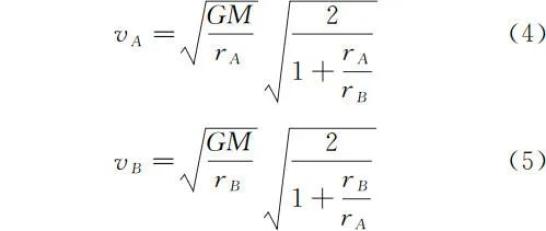
若要计算从近地点到远地点所用的时间，可根据开普勒第三定律得

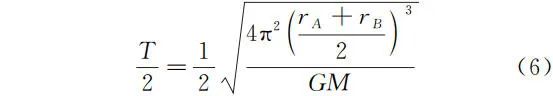
1.2 飞船喷气变轨时消耗燃料与速度变化关系的导出

依据动量守恒，并假设火箭发动机连续地排出燃料，Konstantin Tsiolkovsky 提出了火箭方程，把火箭速度变化量与火箭的初始质量和剩余质量联系了起来[5]

其中，v相对 为气体相对火箭的速度大小。由该式可以看出，Δv 越大，则消耗燃料也越多。

1.3 火箭在以双曲轨道逃逸时从椭圆轨道近地点 rj 到 r 位置处所需时间 t(r) 关系的导出

由能量守恒

，又由角动量守恒 h = rvθ，有

。又因为在椭圆轨道近地点处或圆轨道任一点处有 vr = 0，故有

，其中，rj 为椭圆轨道近地点或圆轨道上一点到中心天体球心的距离。再代回上式中有

，取倒数后两边积分得

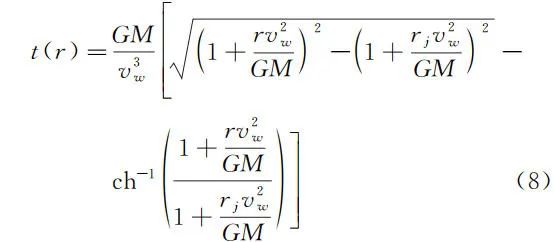
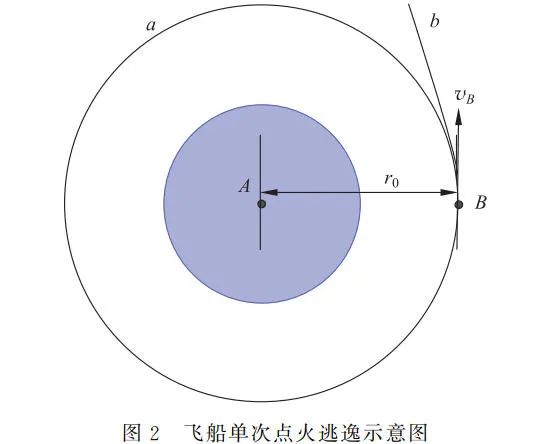
1.4 单次点火逃逸理论分析

如图 2 所示，单次逃逸即在圆轨道 a 上 B 处，单次点火后直接进入双曲轨道 b 逃逸出地球，由式(2)有点火加速后达到的速度

，又

，故有单次点火逃逸的点火前后速度变化量

1.5 Oberth 效应——两次点火逃逸理论分析

Oberth 效应是指当航天器的初始速度越大时，增加相同的 Δv 后航天器的比动能增加得越大。该效应可用于轨道捕获，例如在朱诺探测器进入木星轨道时，就用到了该技术[6] 。近年来国内外都有学者对此效应进行了分析与讨论[7,8]。

如图 3 所示，Oberth 方法是让飞船在圆轨道 c 上某点 C 时先向运动方向喷气减速使其降至离地球更近的椭圆轨道 d 上，接着在近地点 D 处再进行一次向运动反方向的喷气加速进入双曲轨道 e 从而完成逃逸过程。

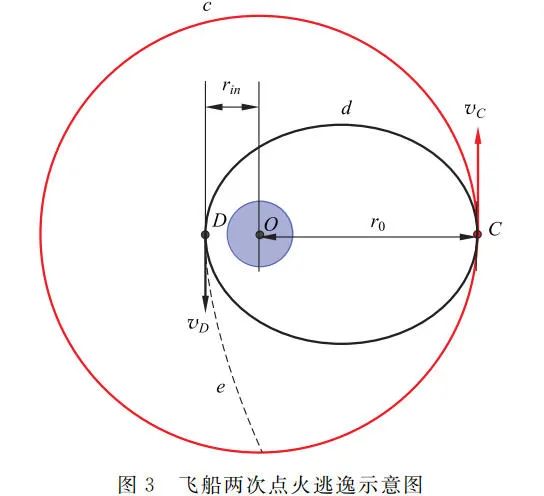
在第一次喷气减速点 C 前后，减速前速度

，又由式(4)可得减速后速度

，故两次点火逃逸方式的第一次点火前后速度变化量

。而在第二次喷气加速点 D 前后，由式(5)可得加速前速度

，又由式(2)可得加速后速度

，故有两次点火逃逸方式的第二次点火前后速度变化量

。

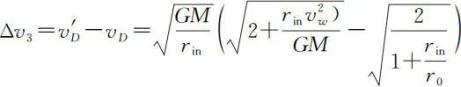
总的速度变化大小为

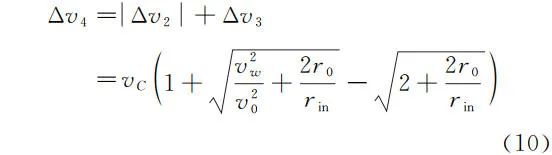
1.6 Edelbaum 效应——三次点火逃逸理论分析

如图 4 所示，三次点火逃逸的方案为先让飞船喷气加速使其升至离地球更远的椭圆轨道上，接着在远地点再喷气减速降至离地球较近的椭圆轨道上，最后在运动至近地点时进行第三次加速逃逸。

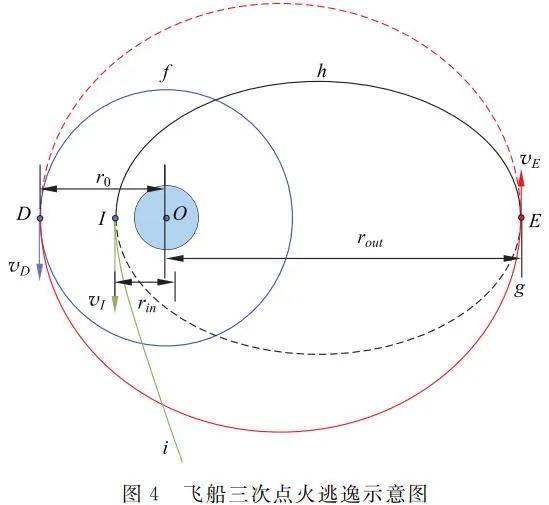
在第一次喷气加速点 D 前后，对圆轨道 f 上有点火加速前速度

，对椭圆轨道 g，由式(5)可得加速后速度

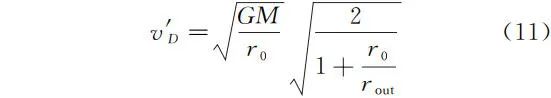
故三次点火逃逸方式的第一次点火前后速度变化量

。在第二次喷气减速点 E 前后，由式(4)对椭圆轨道 g 可得喷气前

由式(4)对椭圆轨道 h 可得喷气后速度有

故三次点火逃逸方式的第二次点火前后速度变化量

。在第三次喷气加速点 I 前后，由式(5)对椭圆轨道 h 可得喷气前速度

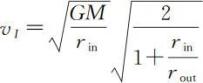
，又由式(2)可得喷气后速度

故有三次点火逃逸方式的第三次点火前后速度变化量

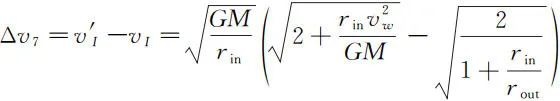
因此三次点火逃逸方式总的速度变化大小为:（由于速度变化的大小对应着燃料消耗的多少，因此减速导致的 Δv6 取绝对值）

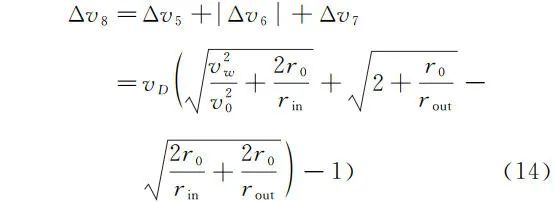
2 VPython 数值模拟

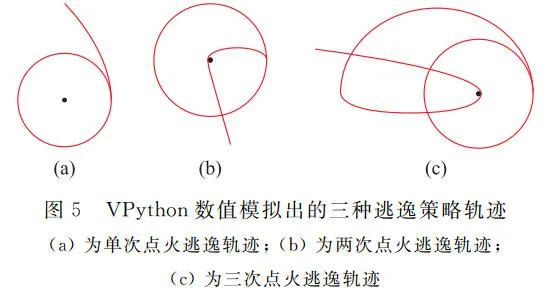
为了检验理论的正确性，可以用 VPython 进行数值模拟仿真实现三种逃逸策略。图 5 所示是用 VPython 进行数值模拟仿真出的三条天体运行轨迹。下面着重说明 Edelbaum 效应的仿真模拟方法。

首先，录入如图 6 所示代码 1~3 行，导入 VPython 库并设置背景。

接着是模拟 Edelbaum 效应代码的参数设置部分，如图 7 所示，其中第 15 行由式(11)得到，第 16、19 行由式(6)得到，第 17 行由式(12)得到，第 20 行由式(13)得到。为了方便的同时又不影响检验理论的正确性，此处非关键参数如万有引力常量和天体质量等都设为 1。

然后如图 8 所示 21~24 行代码绘制了中心天体、飞船以及初始状态下的飞船速度矢量和飞船加速度矢量。

最后，如图 9 所示 25~43 行代码通过 while 语句让其在运动过程中采用欧拉法进行对速度矢量和位置矢量的实时更新。运动中结合前面计算过的时间，通过三个 if 指令让飞船在到达相应的位置处进行点火变速，运行后最终可以观察到图 5 最右边的轨迹。该模拟结果的运动情况和前面理论分析一致，由此可验证理论的正确性。

3 GeoGebra 作图分析三种逃逸方式在燃料消耗上的大小关系

接下来，再通过 GeoGebra 作图比较三种逃逸方式在效率上的差别。由式(7)可知，Δv 越大，则消耗燃料也越多。因此比较三种逃逸方式 Δv 的大小即可比较三种逃逸方式在燃料消耗上的区别。设

，则式(9)、式(10)、式(14)都可以表达成

与

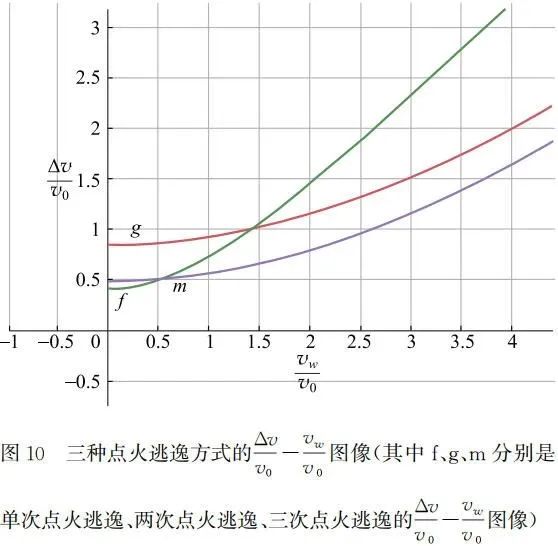
的函数。通过 GeoGebra 作图得到如图 10 所示的图像。其中 f、g、m 分别是单次点火逃逸、两次点火逃逸、三次点火逃逸的

图像。由图像可以看出，当到达无穷远时的速度 vw 接近于 0 时，单次点火逃逸最省燃料，三次点火逃逸次之。而当到达无穷远时的速度 vw 较大时，三次点火逃逸最省燃料，而两次点火逃逸次之。

4 GeoGebra 作图分析三种逃逸方式在所用时间上的大小关系

由于三种逃逸方式仅涉及双曲轨迹上的时间计算以及椭圆半周期的时间计算，因此可由式(6)、式(8)得到三种逃逸方式从 r0 开始运行到 r 位置处所需的时间 ( r > r0 )。设 T0 为在半径为 r0 的圆形轨道上运行的周期。

对单次点火逃逸，由式(8)可得

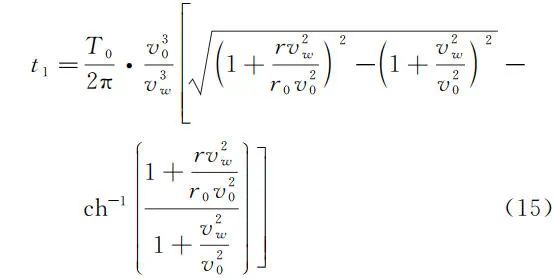
对两次点火逃逸，由式(6)、式(8)可得

对三次点火逃逸，由式(6)、式(8)可得

观察式(15)、式(16)、式(17)可见三式都可以表达成

与

的函数。设 rin = 0.05r0，rout = 2.5r0，r0 = 7.5，G = 1，M = 1，

，

，vw = 0.3v0 通过 GeoGebra 作图得到如图 11 所示的图像.其中 n、o、p 分别是单次点火逃逸、两次点火逃逸、三次点火逃逸的

图像。

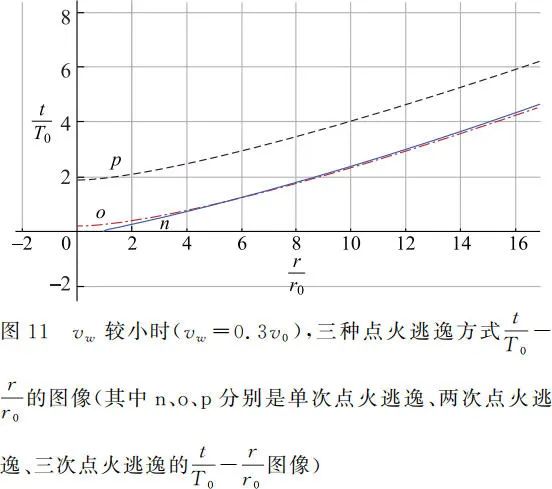
由图像可以看出，当 vw 较小且 r 较小时，单次逃逸所需时间最短，其次是两次点火逃逸用时短，但当 r 较大时，两次点火逃逸用时短。

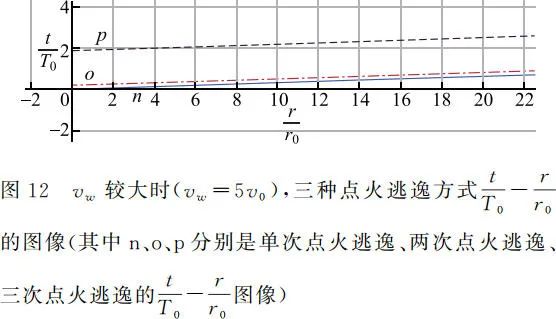
再令 vw = 5v0，得到当 vw 较大时的图像如图 12 所示。由图像可以看出，此时在 r 一定时，单次点火逃逸用时短，两次点火逃逸次之，三次点火逃逸用时最长。

5 结语

通过本文上述的讨论可以发现三种点火逃逸方式在各种情况下各有优劣，若当到达无穷远时的速度 vw 接近于 0 时，单次点火逃逸最省燃料，而当到达无穷远时的速度 vw 较大时，三次点火逃逸最省燃料。当 vw 较小且 r 较小时，单次逃逸所需时间最短，而在 r 较大时，两次点火逃逸用时短。当 vw 较大时，单次点火逃逸用时短，三次点火逃逸用时最长。因此人造飞船逃逸地球时，可针对需求来选择逃逸方式以达到最优解。

参考文献

[1]OBERTH H. Ways to spaceflight[M]. National Aeronautics and Space Administration, 1972.

[2]BLANCO P R, MUNGAN C E. High-speed escape from a circular orbit[J]. American Journal of Physics, 2021, 89(1): 72-79.

[3]ADAMS R , RICHARDSON G. Using the Two-Burn Escape Maneuver for Fast Transfers in the Solar System and Beyond[C]//Aiaa/asme/sae/asee Joint Propulsion Conference & Exhibit. 2013.

[4]EDELBAUM T. Some extensions of the Hohmann transfer maneuver[J]. American Rocket Society J. 29, 864-865.

[5]PHILIP R. BLANCO, Carl E. Mungan. High-speed escape from a circular orbit[J]. American Journal of Physics, 89, 72.

[6]CROCKETT C. Juno Now in Orbit around Jupiter[J]. Science news, 2016, 190(2): 14-14.

[7]BLANCO P, MUNGAN C. Rocket propulsion, classical relativity, and the Oberth effect[J]. The Physics Teacher, 57, 439-441.

[8]李永乐.飞船喷气变轨时需要消耗多少能量[J]. 物理通报, 2017(8): 43-45.

LI Y L. How much energy is consumed during airship varies its orbit by jetting gas[J]. Physics Bulletin, 2017(8): 43-45. (in Chinese)

[9]高翔. 圆锥曲线轨道上行星运动时间计算[J]. 大学物理, 2009, 28(2): 47-48, 56.

GAO X. Calculation of time of a planet in conic curved orbits[J]. College Physics, 2009, 28(2): 47-48, 56. (in Chinese)

[10]周国全. 平方反比有心力作用下的二体系统的一套初等教案[J]. 物理与工程, 2018, 28(5): 39-43+49.

ZHOU G Q. A set of preliminary teaching plan for two-body systems under inverse square central force[J]. Physics and Engineering, 2018, 28(5): 39-43+49. (in Chinese)

基金项目：本文系云南省哲学社会科学规划教育学项目“基于 GeoGebra 的高中物理可视化教学资源开发及教学融合研究”阶段性研究性成果（项目编号：AD20003）。

作者简介：金惠吉，男，研究兴趣为物理教育技术、数值模拟、数学建模等，曾获 2020 年高教社杯全国大学生数学建模竞赛国家一等奖。

通讯作者：陈超，男，主要从事中学物理教学与研究，redchiefok@qq.com。

引文格式: 金惠吉, 陈超, 杨祺. 人造飞船逃逸地球三种方法的理论分析与数值模拟[J]. 物理与工程, 2023, 33(1): 43-49.

Cite this article: JIN H J, CHEN C, YANG Q. Theoretical analysis and numerical simulation of three methods of escape from earth by artificial spacecraft[J]. Physics and Engineering, 2023, 33(1): 43-49. (in Chinese)

END

更多精彩文章请点击下面“蓝字”标题查看：

2023年全国高等学校物理基础课程教育学术研讨会 会议纪要2023 年全国高等学校物理基础课程青年教师讲课比赛在喀什大学举办全国大学物理实验教学对口支援（智力援疆）研讨会在新疆师范大学举办王青教授：理解王中林院士“拓展的麦克斯韦方程组”“碰瓷”麦克斯韦：伽利略协变和洛伦兹协变电磁场论趣谈热点：运动介质洛伦兹协变电磁理论2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授：源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感：教育中的现实和远方王青教授：昨晚（6月9日），清华电动力学期末考试朱邦芬院士：“减负”误区及我国科学教育面临的挑战《物理与工程》2022年第6期目录乐永康：新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡：对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士：从基础科学班到清华学堂物理班朱邦芬院士：对培养一流拔尖创新人才的思考李学潜教授：物理是一种文化李学潜教授：如何帮助物理系学生迈过从高三到大一这个坎穆良柱：物理课程思政教育的核心是科学认知能力培养穆良柱：什么是物理及物理文化？穆良柱：什么是ETA物理认知模型穆良柱：什么是ETA物理教学法吴国祯教授：我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写

陈佳洱，赵凯华，王殖东：面向21世纪，急待重建我国的工科物理教育王亚愚教授：清华物理系本科人才培养理念与实践葛惟昆教授：关于中外人才培养的几点思考安宇教授：为什么传统的课堂讲授模式需要改变安宇教授：其实教学就是积累的过程刘玉鑫教授：关于本科生物理基础课程教学和教材编著的一些思考沈乾若：重创理科教育的美加课程改革Henderson C：美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊，是中国科技核心期刊，1981年创刊，欢迎踊跃投稿，期刊投审稿采编平台：

http://gkwl.cbpt.cnki.net

欢迎关注

《物理与工程》微信公众号

原标题：《人造飞船逃逸地球三种方法的理论分析与数值模拟》

阅读原文