基于 Hirota方法探求非零边界条件下 MNLS/DNLS方程的孤子解

原创 周国全 雒润嘉 等 物理与工程

摘要

Hirota双线性导数变换处理非线性偏微分方程，是一种比反散射变换更为方便的直接方法。本文展示了Hirota双线性导数变换法应用于求解非线性可积方程的一般手续，以非零驻波边界条件下修正的非线性薛定谔（MNLS）方程为例，探求其孤子解；再通过简单的参数归零法直接得到导数非线性薛定谔（DNLS）方程在非零常数边界条件下的相应孤子解，亮/暗孤子解随时间和空间变量的演化也通过图像加以演示, 所得孤子解与反散射方法得到的结果一致相符。

关键词 孤子;非线性方程;修正的非线性薛定谔方程；导数非线性薛定谔方程;Hirota方法;Hirota双

SOLITON SOLUTION OF MNLS/DNLS EQUATION WITH

NONVANISHING BOUNDARY CONDITION BASED ON

HIROTA METHODZHOU GuoquanLUO RunjiaQI Ying

(Department of Physics, Wuhan University, Wuhan, Hubei 430072)

Abstract Hirotas bilinear derivative transformation is a direct method which is more convenient than the inverse scattering transform to deal with a nonlinear partial deferential equation. Based on Hirotas method, the soliton solutions of the modified nonlinear Schrödinger (MNLS) equation under standing wave boundary condition, are obtained; and by simple method of parameter vanishing, the corresponding soliton solutions of the derivative nonlinear Schrödinger (DNLS) equation under constant nonvanishing boundary condition, are gotten, which allows the existence of both bright and dark solitons. The evolution of bright/ dark-soliton solutions in time and space is demonstrated in figures. The results are consistent with what were obtained by the inverse scattering transform.

Key wordssoliton；nonlinear equation；modified nonlinear Schrödinger equation；derivative nonlinear Schrödinger equation；Hirota method；Hirotas bilinear derivative transformation

自然界存在两类稳定的波动状态，一类稳定波动存在于线性且无色散的均匀媒质中，因为非线性效应和色散效应都会破坏波的稳定性。但是，当传波媒质的非线性效应与色散效应达到一种精致而稳定的平衡并相互抵消的时候，媒质中又会产生一种孤立、稳定的局域波动，称为孤立波（solitary wave），即第二类稳定传播的波动现象[1]。描述这类孤立、稳定且局域的波动现象在时空中的演化过程的偏微分方程，称为可积非线性微分方程。可积非线性方程既有非线性项，又有色散项，可以改写成一对关于时空变量的线性演化方程（所谓Lax pair）的可积条件[1]，也称为相容性条件（compatibility condition），或者零曲率条件（zero-curvature condition）。一些稳定的孤立波之所以被称为孤子（soliton），是因为它们的传播呈现一种经典的准粒子运动状态，其相互间的碰撞过程类似于弹性粒子之间的碰撞。孤子种类很多，诸如亮/暗孤子、呼吸子、高阶孤子、流氓波（rogue wave），并且各具不同的物理背景，比如光纤中传播的光孤子，等离子体中传播的阿尔芬孤波，QCD的规范量子场微分方程的真空瞬子（instanton），等等。本文专注于讨论非线性光纤光学中的光孤子理论。

光孤子理论应用于光纤通信领域，十分重要，广受关注[1]。将在单模光纤中传播的皮秒或飞秒级超短脉冲激光波包函数记为u(x,t)（正比于激光脉冲的电场分量），在考虑了自相位调制和自陡变效应以后，u(x,t)满足修正的非线性薛定谔(MNLS)方程[2]

其中含参数γ的项量化体现了电场引起的非线性克尔效应，注意实际上x是时间变量，而t是空间变量, （这是为了与其他领域的某些非线性模型拥有统一的微分方程，从而发展出统一的解决方案[1-3]）。若将参数γ归零或进行类规范变换[3,4]，MNLS方程(1)可演变为导数非线性薛定谔(DNLS)方程

上述DNLS方程(2)中的v(x,t)可用于描述等离子体中的阿尔芬孤波和一些铁磁/反铁磁介质中传播的弱非线性电磁波[5-8]。

探求非线性可积方程的各类孤子解的常见方法有反散射（inverse scattering）变换，Daboux变换，Bcklund变换等间接方法，和Hirota双线性导数变换等直接方法。对于非零边界条件下DNLS方程的求解，使用Bäcklund变换法将会得到矩阵形式解，它并不适合直观地演示孤子的相互作用[9]；而反散射变换法将会遇到黎曼面上的多值问题和发散的围道积分，迂回曲折，繁难费时。Hirota方法更为直观简便，它结合摄动微扰技术，对方程的非零边界条件的预设更少，能够求解各类不同的孤子解。本文即采用Hirota双线性导数变换法求解MNLS/DNLS在非零特殊边界条件下的亮/暗孤子解。

在MNLS方程提出后不久，它在零边界条件下的孤子解已被学者们用反散射变换法求得[1,2]。文献[6]使用Hirota方法求得了MNLS方程在平面波背景下的特殊流氓波解。至于DNLS方程，文献[11-13,4,14-16]分别用不同方法求出了该方程在零/非零边界条件下的亮/暗单孤子或N孤子解，纯孤子/呼吸子或混合孤子解；文献[17]运用Hirota方法求得DNLS方程的特殊流氓波解和空间周期解。迄今未见有人尝试用Hirota方法探求非零边界条件下的MNLS/DNLS方程的亮/暗孤子解或呼吸子解。本文以MNLS方程为例，介绍了Hirota双线性导数变换的定义与性质，及其应用于非线性可积方程的一般手续与技巧；尝试并成功地求解了MNLS方程在驻波边界条件下的孤子解，并在其微扰参数γ趋近于零时，使该解退化为DNLS方程在常数边界条件下的亮/暗孤子解。最后我们还讨论了微扰强弱——参数γ的大小、背景波振幅对亮/暗孤子行为的影响。

1 Hirota双线性导数变换

Hirota最先引入双线性导数变换——即一个双D算符，用来处理一些偏微分方程[18,19]，其定义为

其中符号•代表f、g之间的有序乘积，当m或n为1时可省去上标，例如

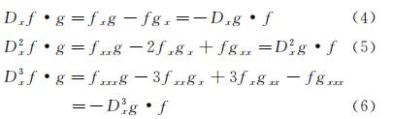
易证Hirota双线性导数变换具有若干重要性质：

性质1：

特别地，当m+n为奇数时，

性质2：若C为常数，有

性质3：设ηj=ωjt+kjx+η0j，其中j=1，2，ωj和kj均为复常数，则有

推论，具有相同系数的线性指数函数的双线性导数为零，即当 ω₁=ω₂或k₁=k₂时

为应用上述D算符的便利的性质，将方程转化为 仅含双线性 D算符而不含其他普通偏导算符的形 式,即双线性形式,分离变量后将其拆解为双线性方程组。

2 MNLS/DNLS方程的双线性导数形式及其孤子解

参考MNLS/DNLS方程的孤子解所具有的典型形式[4,6-8,12,14,16]

本文将上式作为MNLS方程未知解函数的变换形式。据定义(3)，可以给出如下两个常用的双线性导数变换公式

运用以上公式，可得

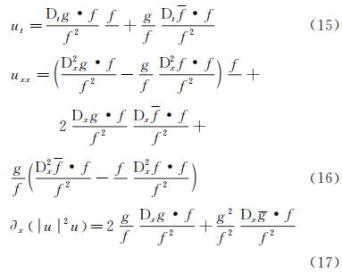
将上述各式代入MNLS方程，可得

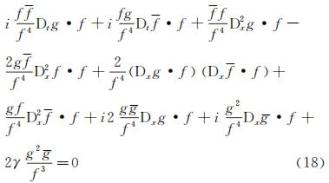
将上式两边分别乘以f4, 合并化简得仅含D算符的双线性导数形式

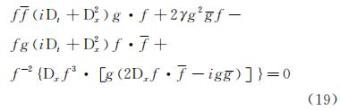
不同于零边界条件的处理方法[15]，为得到非零边界条件下的解，引入参数λ，将上式(19)拆分为如下双线性方程组：

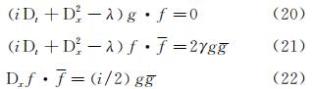
其中λ的取值取决于函数f、g的函数形式、γ的取值及其正负，以及u(x,t)在无穷远处的边界条件。先将函数f 、g展开为摄动微扰参数ε的无穷级数

代入式(20）~式（22)后，再将变换后的方程展开为摄动微扰参数ε的无穷级数，合并整理，比较方程两边参数εn的同幂项，得到

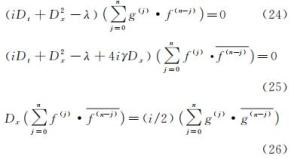
其中式(25)由式(21)，式(22)导出。n可取0,1,2,…,∞，即有无穷组这样的方程。

现在设定f(i)=0,i≥2，g(i)=0,i≥2。这是使得式(23)中仅剩对应于单孤子解的相关级数项,同时满足双线性方程，即单孤子截断的充分不必要条件。换言之，Hirota方法选择了单孤子解[14]。涉及到式（24）~式（26）中ε=0,1,2三组共9个方程：

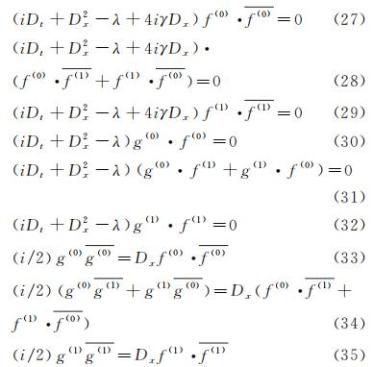
考虑到Hirota双线性导数变化法探求非线性可积方程的孤子解的关键手段是将未知函数f，g展开为线性指数函数的级数，不失一般性，将f,g的各阶微扰项写作线性指数函数。对于形如

的指数函数，从双线性导数方程

仅能得到函数h(x,t)的辐角的变量前的参数ω1、k1的相关方程。式(27)正是这种形式，即无法从中得到f(0)的辐角中的常数项和模的信息，不妨将它们吸收纳入g(0)的表达式中。鉴于式(12)的u表达式中含有f, g之商，此举不失一般性，即假设

。f(0),f(1)分别满足的式(27)、式(29)完全一致，且形如式(36)，即f(0)与f(1)的辐角满足同一微分方程，可以假设f(0),f(1)的辐角仅相差一常数：

其中所有常参数ω0,k0,ξ(0)1,τ,κ,η(0)均为实数。

将g(0)写作

，其中a0,b0为实数，ρ可以取复数值。将f(0),f(1)代入式(33)、式(35)，得到|g(1)|2=|ρ|2e2η，不妨将g(1)写作

其中a1,b1,α(0)1为实数。再将f(0),f(1), g(0),g(1)代入式(32)，可得

代入式(30)，可得

不妨假设a0=a1,b0=b1，得到f、g的表达式

其中

当我们需要eη →+∞，在x→±∞或t→±∞时，(取决于时间空间变量前的系数正负性,例如 在 τ>0,κ>0时,x→+∞或t→+∞),我们有

而当边界条件使得e η →0时,u 的边界极限取值与 上式(44)仅差一常数相因子。由以上分析可见, 若α0 与ξ0 简单地取x,t的线性函数,通过 Hirota 双线性导数变换法可以求解的非零边界条件的类 型有常数边界、平面波边界、驻波或正/余弦边界。要使波函数在无穷远处趋近于驻波边界条件,即 只含时间变量x,即让α0 -3ξ0 仅随时间参量x 改变,可以假定α0,ξ0 中t的参数均为零,即ω0= a0=0。值得注意的是,分析发现,使用 Hirota方 法无法得到 MNLS在常数边界条件的解,因为它 会导致式(27)与式(30)两式矛盾。

将解 中 f (0) 和 g (0) 代 入 式 (27),式 (30), 式(33),同时考虑边界条件上述约束,得到

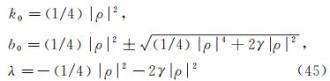
将其中各参数表达为ρ 与γ 的函数,以便根据给 定的具体边界条件与微扰项γ 值来拟合理论解中 的参数。

将获得的f (0),f (1),g (0),g (1)表达式代入式(28), 式(31),式(34),得到含

、

、τ、κ 四个未知 数的三个方程,不妨将其余三者用ξ1 (0) 表示:

而式(29),式(32),式(35)中包含的信息在寻找孤子解的过程中已经运用。至此我们得到MNLS方程在驻波边界条件下的单孤子解

其中η=τt+κx+η (0)，各常数参数取值见式(45）~式（47)。将ρ、γ、

视作可调节参数。取特殊参数值作图，如图1所示，它对应着在波导中传播的超短脉冲的电场的绝对值的时空演化。其中(a)单孤子振幅绝对值大于背景波，为亮孤子；(b)中单孤子振幅绝对值小于背景波，为暗孤子。以图1(a)为例，取t=t0 （-∞

当MNLS方程的参数γ 取零时，前述孤子解退化为DNLS方程的孤子解

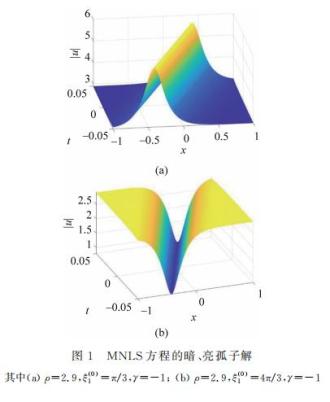
其中

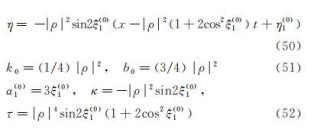
γ =0时, 上面的解满足边界条件u=ρ，当e η→+∞，即x →±∞或t →±∞时（取决于时间空间变量前的系数正负性，例如在τ >0,κ >0时，x→+∞或t→+∞），即MNLS的驻波/简谐波边界条件, 在γ趋近于零时对应于DNLS的非零常数边界条件。这与文献[8,14]利用改进的反散射法得到的常数边界条件下DNLS方程的纯孤子解一致。两种方法对比可知，本文Hirota方法得到的DNLS方程的孤子解中的复常参数

对应于反散射法[14]中围道积分的极点。如图2所示，当复常参数取不同的特殊值（相差π的相位）时，可分别得到亮/暗孤子解。

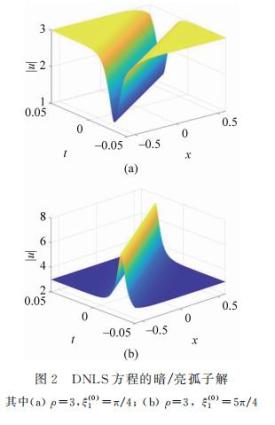
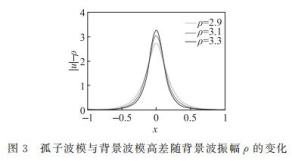
当参数γ 趋近于0 (但不等于0) 时，MNLS方程的孤子解趋近于DNLS方程的孤子解。为探究γ 不为零带来的新特点，固定ρ，将解减去背景波的影响，分析发现随着γ 趋近于零，孤子变高变窄，反之则变矮变宽，即微扰项让DNLS方程的孤子解弥散。另一方面，如图3所示，随着背景波振幅ρ 的增加，孤子变高变窄，即更剧烈的背景振荡将更突显孤子的存在。注意到γ 作为MNLS方程在DNLS方程基础上的微扰强度的度量，对MNLS方程单孤子解的影响远不及背景波振幅的影响。

3 结语

本文展示了运用Hirota 双线性导数变换法求解非线性可积方程的全部手续与过程；以MNLS方程为例求出其在驻波边界条件下的亮/暗单孤子解。通过参数归零法使MNLS方程退化为DNLS方程时，该解自然地变为DNLS方程在常数边界条件下的亮/暗孤子解，并与运用修改的反散射法求得的孤子解完全一致。通过对比，找到了两种方法等价结果的对应参数关系。同时研究表明，微扰项导致孤子解的弥散，更剧烈的背景振荡将更突显孤子的存在。

参考文献

[1]ABHINAV K, GUHA P, MUKHERJEE I. Study of quasi-integrable and non-holonomic deformation of equations in the NLS and DNLS hierarchy[J/OL]. Journal of Mathematical Physics, 2018, 59(10). DOI:10.1063/1.5019268.

[2]SONG Y, SHI X, WU C, et al. Recent progress of study on optical solitons in fiber lasers[J/OL]. Applied Physics Reviews, 2019, 6(2). DOI:10.1063/1.5091811.

[3]CHEN Z Y, HUANG N N. Explicit N-soliton solution of the modified nonlinear Schrodinger equation[R]//PHYSICAL REVIEW A: 卷41. 1990.

[4]LASHKIN V M. N-soliton solutions and perturbation theory for the derivative nonlinear Schrdinger equation with nonvanishing boundary conditions[J/OL]. Journal of Physics A: Mathematical and Theoretical, 2007, 40(23): 6119-6132. DOI:10.1088/1751-8113/40/23/008.

[5]KHALIQUE C M, PLAATJIE K, ADEYEMO O D. First integrals, solutions and conservation laws of the derivative nonlinear Schrdinger equation[J/OL]. Partial Differential Equations in Applied Mathematics, 2022, 5. DOI:10.1016/j.padiff.2022.100382.

[6]唐宇轩, 周国全. 用Hirota双线性导数变换法求MNLS方程的Rogue波解[J]. 数学物理学报, 2023, 43(A(1)): 132-142.

TANG Y X， ZHOU G Q. The Rogue wave solution of MNLS/DNLS equation based on Hirota's bi-linear derivative transformation[J]. Acta Mathematica Scientia, 2023, 43, A(1): 132-142. (in Chinese)

[7]CAI H. Research about MNLS Equation and DNLS Equation[D]. Wuhan: Wuhan University, 2005.

[8]CHEN X J, YANG J, LAM W K. N-soliton solution for the derivative nonlinear Schrdinger equation with nonvanishing boundary conditions[J/OL]. Journal of Physics A: Mathematical and General, 2006, 39(13): 3263. https://dx.doi.org/10.1088/0305-4470/39/13/006. DOI:10.1088/0305-4470/39/13/006.

[9]MJLHUS E, HADA T. Nonlinear waves and chaos in space plasmas[M]. Tokyo, 1997.

[10]CHEN X J, YANG J, LAM W K. N-soliton solution for the derivative nonlinear Schrdinger equation with nonvanishing boundary conditions[J/OL]. Journal of Physics A: Mathematical and General, 2006, 39(13): 3263-3274. DOI:10.1088/0305-4470/39/13/006.

[11]KAUP D J, NEWELL A C. An exact solution for a derivative nonlinear Schrdinger equation[J/OL]. Journal of Mathematical Physics, 1977, 19(4): 798-801. DOI:10.1063/1.523737.

[12]ZHOU G Q, HUANG N N. An N-soliton solution to the DNLS equation based on a revised inverse scattering transform[J]. Journal of Physics A: Mathematical and Theoretical, 2007, 40.

[13]NIAN-NING HUANG, ZONG-YUN CHEN. Alfven solitons[J/OL]. Journal of Physics A: Mathematical and General, 1990, 23(4): 439. https://dx.doi.org/10.1088/0305-4470/23/4/014. DOI:10.1088/0305-4470/23/4/014.

[14]ZHOU G Q. Explicit breather-type and pure N-soliton solution of DNLS+ equation with nonvanishing boundary condition[J]. Wuhan University Journal of Natural Sciences, 2013, 18: 147-155.

[15]ZHOU G Q, BI X T. Soliton solution of the DNLS equation based on Hirotas bilinear derivative transform[J]. Wuhan University Journal of Natural Sciences, 2009, 14: 505-510.

[16]LI X J, ZHOU G Q. Mixed breather-type and pure soliton solution of DNLS equation[J/OL]. Wuhan University Journal of Natural Sciences, 2017, 22(3): 223-232. https://doi.org/10.1007/s11859-017-1239-0. DOI:10.1007/s11859-017-1239-0.

[17]ZHOU G Q, LI X J. Space periodic solutions and rogue wave solution of the derivative nonlinear Schrdinger equation[J/OL]. Wuhan University Journal of Natural Sciences, 2017, 22: 373-379. DOI:10.1007/s11859-017-1261-2.

[18]HIETARINTA J, NIMMO J. Foreword[M]//BOLLOBAS B, FULTON W, KATOK A, et al. The Direct Method in Soliton Theory. New York: Cambridge University Press, 2004: vii-viii.

[19]HIROTA R. The direct method in soliton theory[M]. New York: Cambridge University Press, 2004.

作者简介:周国全,男,武汉大学副教授,研究方向为非线性可积方程及孤子理论,电磁场理论,zgq@whu.edu.cn。

引文格式: 周国全，雒润嘉，齐蓥. 基于Hirota方法探求非零边界条件下MNLS/DNLS方程的孤子解[J]. 物理与工程，2023，33（4）：79-84.

Cite this article: ZHOU G Q, LUO R J, QI Y. Soliton solution of MNLS/DNLS equation with nonvanishing boundary condition based on Hirota method[J]. Physics and Engineering, 2023， 33（4）：79-84. (in Chinese）

END

更多精彩文章请点击下面“蓝字”标题查看：

CALL FOR PAPERS｜《物理与工程》征稿量子世纪年中国大学物理教育MOOC联盟2023年工作会议（扩大）暨典型案例交流会 会议纪要2023年全国高等学校物理基础课程教育学术研讨会 会议纪要2023 年全国高等学校物理基础课程青年教师讲课比赛在喀什大学举办全国大学物理实验教学对口支援（智力援疆）研讨会在新疆师范大学举办王青教授：理解王中林院士“拓展的麦克斯韦方程组”“碰瓷”麦克斯韦：伽利略协变和洛伦兹协变电磁场论趣谈热点：运动介质洛伦兹协变电磁理论2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授：源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感：教育中的现实和远方王青教授：昨晚（6月9日），清华电动力学期末考试朱邦芬院士：“减负”误区及我国科学教育面临的挑战《物理与工程》2023年第3期目录乐永康：新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡：对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士：从基础科学班到清华学堂物理班朱邦芬院士：对培养一流拔尖创新人才的思考李学潜教授：物理是一种文化李学潜教授：如何帮助物理系学生迈过从高三到大一这个坎穆良柱：物理课程思政教育的核心是科学认知能力培养穆良柱：什么是物理及物理文化？穆良柱：什么是ETA物理认知模型穆良柱：什么是ETA物理教学法吴国祯教授：我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写

陈佳洱，赵凯华，王殖东：面向21世纪，急待重建我国的工科物理教育王亚愚教授：清华物理系本科人才培养理念与实践葛惟昆教授：关于中外人才培养的几点思考安宇教授：为什么传统的课堂讲授模式需要改变安宇教授：其实教学就是积累的过程刘玉鑫教授：关于本科生物理基础课程教学和教材编著的一些思考沈乾若：重创理科教育的美加课程改革Henderson C：美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊，是中国科技核心期刊，1981年创刊，欢迎踊跃投稿，期刊投审稿采编平台：

http://gkwl.cbpt.cnki.net

欢迎关注

《物理与工程》微信公众号

继续滑动看下一个

基于 Hirota方法探求非零边界条件下 MNLS/DNLS方程的孤子解原创 周国全 雒润嘉 等 物理与工程 轻触阅读原文

物理与工程 赞 分享 在看 写留言 向上滑动看下一个

原标题：《基于 Hirota方法探求非零边界条件下 MNLS/DNLS方程的孤子解》

阅读原文