【复材资讯】颗粒增强镁基复合材料流体行为与颗粒分散的数值模拟

摘 要

采用ANSYS Fluent有限元分析软件模拟了在不同倾角（30°、45°、60°、90°）搅拌桨的作用下，坩埚内部流场的结构及其变化特点。通过建立k-ε湍流模型和Euler-Euler多相流模型分析了坩埚内涡流分布规律，并通过模拟颗粒的分散状况进行验证。结果表明，直叶桨坩埚内部流场流速快，但被桨叶搅拌作用分割为上下两个循环区域（双环型流型），混乱程度低，颗粒的分散效果不佳。斜叶桨表面内旋作用明显，矢量混乱度高，颗粒分散第一阶段的效率高；斜叶桨坩埚内部存在轴向流，可形成一体的循环区域（单环型流型），使得颗粒的流动区域更大，分散效果更好。

作者

郭子义1, 邓坤坤1, 聂凯波1,王翠菊1, 刘 力2

1.太原理工大学材料科学与工程学院,太原 030024;

2.兴县经开区铝镁新材料研发有限公司,吕梁 033603)

正文

镁基复合材料具有比强度、比刚度高，密度小，高温性能良好等特点，在航空、航天、军事、汽车以及电子等领域具有广阔的应用前景。其中，颗粒增强镁基复合材料因其制备工艺简单、生产成本低、成形性能好，近年来备受研究者青睐［1-3］。颗粒增强镁基复合材料的制备工艺主要有喷射沉积、挤压铸造、高能超声复合以及搅拌铸造法等，其中搅拌铸造制备工艺体系成熟，设备简易且成本较低，适用于制备大尺寸铸件，因此被广泛应用于实际生产［4-10］。

提高颗粒的分散程度，是搅拌铸造镁基复合材料的主要难题。以往研究多从搅拌温度、时间、速度、润湿性等角度出发，探究颗粒分散的优化解［5，8，11-12］，缺乏镁合金熔体的流动行为及颗粒在熔体中分布规律的相关认识。搅拌铸造颗粒增强镁基复合材料以试验研究为主，且多为定性评价［13］，工作量大、效率低且范围窄［14］，不利于颗粒增强镁基复合材料制备和规模化应用。基于数值模拟方法建立搅拌过程中固液混合流场特性与颗粒分布均匀性之间的联系，分析搅拌过程中颗粒分布的规律，对制备颗粒均匀分布镁基复合材料十分必要。

已有研究者基于计算机数值模拟的方法对颗粒在合金熔体中的分布规律进行了初步探索。陶辰亮等［15］使用Fluent软件，模拟研究200、400、600 r/min等3组转速对增强相颗粒分布的影响，并通过试验验证，得出最优搅拌转速为400 r/min。闫禹伯［16］使用FLOW-3D软件模拟1 mm大尺寸颗粒分布情况（实际其颗粒直径约为10 μm），探究最佳的搅拌工艺，并通过试验验证得到机械搅拌法制备SiCp颗粒增强2014Al理想的搅拌速度、搅拌时间以及搅拌深度，分别为450 r/min、15 min和距底3/4处；周超［17］基于CFD（计算流体力学）原理，模拟了B4Cp增强A356合金的过程，确定最佳搅拌速度和最佳搅拌时间为800 r/min和25 min；张福龙等［18］通过VOF（流体体积）模型，模拟得到不易发生卷气的转速范围为200～300 r/min，并通过DPM（离散相位）模型得到颗粒分散均匀的理想搅拌时间为15 min。综上，现有研究主要关注大尺寸颗粒的分散情况，并且较多集中在搅拌工艺的优化方面，而关于搅拌桨形状对流体行为的影响方面报道较少。此外，采用的计算模型多经过大量简化［16，18］，忽略了增强体颗粒流动与合金熔体之间的相互作用，尚不足以指导微小颗粒在镁合金熔体中的分布与调控相关研究。

基于此背景，本研究采用ANSYS Fluent软件对颗粒搅拌熔体流场进行模拟，充分考虑重力、浮力、马格努斯力等作用力的影响以及颗粒间的相互作用，分析搅拌过程中熔体流动规律，构建稳态、瞬态图研究搅拌过程中颗粒分布规律，探索桨叶角度对熔体流动行为的影响以及颗粒在熔体中分散行为的影响，旨在为加深对其了解提供参考。

1 模拟方法

1.1 模型建立和网格划分

采用固液两相流模型对搅拌铸造中颗粒在合金熔体中的分布过程进行数值模拟，通过分析熔体在流动过程中的速度云图、熔体流线图、熔体矢量图以及颗粒受搅拌器作用时间的分散图，研究30°、45°、60°、90°等4组不同角度桨叶对熔体流动及颗粒分散的影响。

坩埚与搅拌桨的二维、三维模型图以及网格划分示意图见图1。坩埚内径D为110 mm，高度H为110 mm，模拟熔体区域高度H1为80 mm，采用长薄叶搅拌桨，其长度为70 mm。依据角度不同设定4组模拟对象，分别为30°搅拌桨组（AG30）、45°搅拌桨组（AG45）、60°搅拌桨组（AG60）和90°搅拌桨组（AG90），搅拌桨转速设为600 r/min。网格采用非均匀化网格，搅拌桨周围1～2 mm区域设置精细网格。在此范围外，适当简化网格设置以便计算。总体网格数量约为50万，经检验网格满足无关性要求。

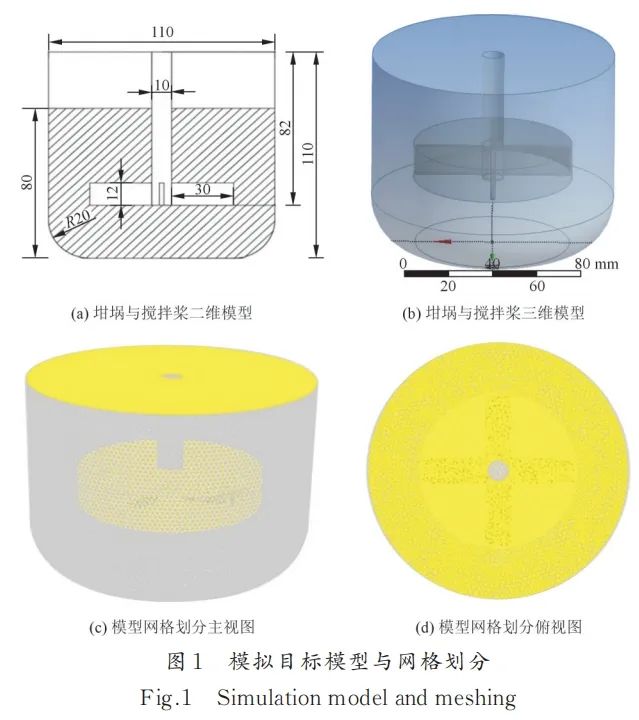图1

1.2 计算方程

1.2.1 流体力学基本方程

流体力学基本方程是计算流体力学（CFD）的核心，其主要包括质量守恒方程、动量方程和能量方程。

镁合金熔体采用连续介质模型的均质熔体，在此基础上其连续性方程为:

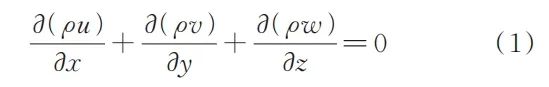式中，ρ为熔体的密度；u、v、w分别为x、y、z方向的速度分量。

动量方程为

式中，ρ为流体密度；F为静压力；τij为雷诺应力；ui、uj为流体速度在i和j方向的分量；gi为重力加速度在i方向的分量。

能量方程为

式中，p为熔体中某点的压强；v为熔体该点的流速；g为重力加速度；h为该点高度；C为常量。

1.2.2 多相流模拟方法与模型

为了充分考虑实际颗粒状况，采用多相流方法进行模拟。该体系主要包括Euler-Lagrange法与Euler-Euler法两大类，其中Euler-Euler法中包括了VOF（volume of fluid）模型、Euler-Euler模型以及Mixture模型 ［19-22，27-32］。

（1） Euler-Lagrange法

在Euler-Lagrange法中熔体流场是在Euler坐标系下求解的，其核心方程为质量守恒方程和动量守恒方程；离散相的运动轨迹部分可通过Lagrange坐标系求解，其核心方程为离散相力平衡方程［23］。熔体相处理为连续相，其运动由Navier-Stokes方程控制；颗粒处理为离散相，其运动由大量颗粒的独立动量方程控制。其中，颗粒轨道方程为［24］：

式中，i、j分别为x、y方向的相对坐标；ρk=nkmk为颗粒相表观密度；τrk为弛豫时间；S为通用形式下方程的源项；Fk,Mi为第k种颗粒的Magnus力；vk为颗粒相的速度。

Euler-Lagrange模型的简化条件较少，可以充分揭示分散相的复杂变化、运动轨迹及反应规律，但是受限于网格与计算条件，该模型仅适用于分散相含量较低的流动，一般要求分散相含量低于10%［25］。

（2） Euler-Euler法

Euler-Euler法是在Euler坐标系下求解颗粒（被视作连续相）与熔体（连续相）的运动［26］，将不同相处理成互相贯穿的连续介质。与Euler-Lagrange法不同，该法核心是对熔体整体在空间上的流动方式与变化进行追踪，填补了Euler-Lagrange模型在分散相浓度较高场合下的限制。

1.3 边界条件与设置

采用ANSYA Fluent软件对坩埚流动场模型进行数值模拟。选择稳态绝对速度基于压力基求解的求解器；选择RNG（Re-normalization Group，RNG）的k-ε湍流模型，壁面函数选择标准壁面函数（Standard Wall Functions，SWF）；镁基复合材料工作状态为高温熔融态，因此熔体材料选择与其物性相似的液体模型，模拟半固态条件；设置好重力，将液面设置为symmetry，将桨杆和搅拌桨设置为wall；设定运动区域转速为搅拌槽顶部俯视，顺时针方向速度为600 r/min，运动区域以外（静止区域）部分速度为0；设置收敛部分残差为10-6，设定公式湍流耗散率、欠松弛因子，其余参数选取默认；开启多相流，选择适合的多相流模型；设置欧拉相位数量、阻力系数、表面张力系数等；设置颗粒与群体平衡模型，最后进行局部和总体初始化。

2 模拟结果与讨论

2.1 不同搅拌桨桨叶角度流场流速云图分布

图2为模拟采集AG30、AG45、AG60和AG90的平面速度云图，见图3。由统计可知，AG30坩埚内部高速区（v∈［1.2，2.0］）、中速区（v∈［0.3，1.2））、低速区（v∈［0，0.3））分别占3.5%、35%、61%；AG45坩埚内部高速区、中速区、低速区分别占3.5%、36%、60%；AG60坩埚内部高中低速区分别占4%、45.2%、50.8%；AG90坩埚内部高中低速区分别占4.1%、53.4%、42.5%。

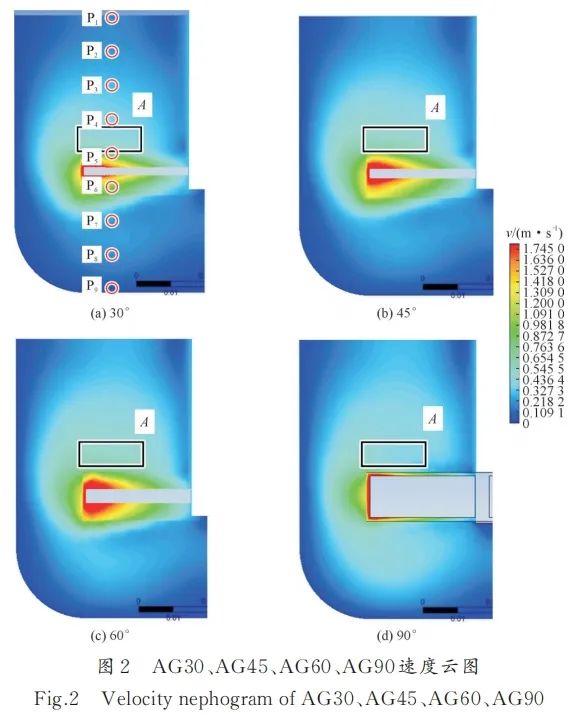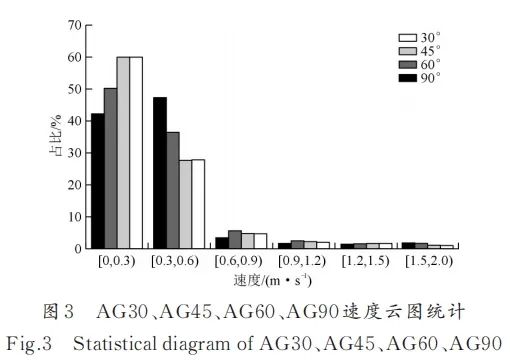图2图3

由图3可知，桨叶角度的变化会影响熔体整体速度，但其对熔体轴向速度的影响尚不清楚。对4类坩埚内部轴向流体的流动速度进行统计，在熔体中心处（距中心1/2坩埚半径处）均匀选取采样点P1～P9并统计流动速度，结果见图4。由图4a知，4组搅拌桨皆在近桨区（距底高度为30 mm）速度最快，在距底高度60 mm以上（熔体表面）或20 mm以下（熔体底部）的位置采样点速度最慢，坩埚底部部分熔体速度几乎为0。熔体轴向速度分布整体较为规律，将轴向速度作差可以进一步得到轴向速度梯度，而速度梯度是形成剪切力的条件，影响颗粒分散效果［33］。因此将采集得到的轴向速度作差，形成速度梯度图，其中速度梯度变化较大的部分见图4b。可以看出，桨叶角度为30°时，熔体速度随采样点高度变化最为平缓，轴向速度梯度较小；当桨叶角度增加为90°时，熔体速度随采样点距底部高度的变化最为明显，轴向速度梯度最大。

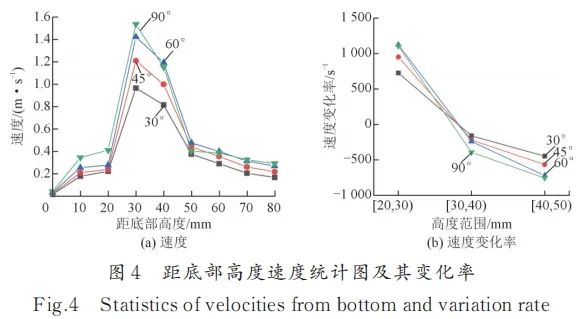图4

2.2 流场矢量图平面分布

图5为各组的流场速度矢量图。可以看出，AG30中C区域存在斜上方向的高速轴向流体（High speed axial fluid， HSAF），见图5a。当桨叶角度增至60°时，C区域斜上方HSAF持续增加，数量增多，见图5b和图5c。然而，当桨叶角度增加至90°时，C区域斜上方HSAF大幅减少，见图5d。HSAF数量排序为：AG60＞AG45＞AG30＞AG90。

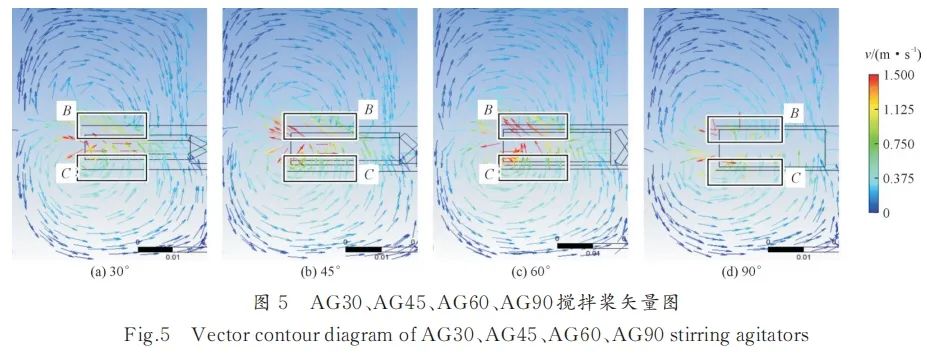图5

2.3 流场流线图分布

通过矢量图可以对熔体某点处瞬时速度大小和方向进行分析，而熔体瞬时质点状态则需要通过流线图来说明［34］。图6为4组搅拌桨三维熔体流线图，D区域为熔体的中心区域，其区域流线密度可以充分反映熔体的流量大小，区域内流线密度为ρ，图中E、F区域分别代表坩埚壁附近上下半熔体的流动趋势。对4组流线图中D区域进行数据统计，发现AG30的ρ值为51.5%；随着桨叶角度增加至45°，ρ值最高为65.1%；当桨叶角度继续增加至60°和90°，AG60和AG90的ρ值分别为59%和46.6%。由上述可知，AG90熔体流经D区流线稀疏；AG45在D区流线最为密集。AG30、AG45、AG60靠近坩埚壁面区（E区域和F区域）部分熔体会发生交流作用。在旋转过程中，E区上半熔体向下流动，F区下半熔体向上流动；AG90熔体在E、F区交流作用最弱。

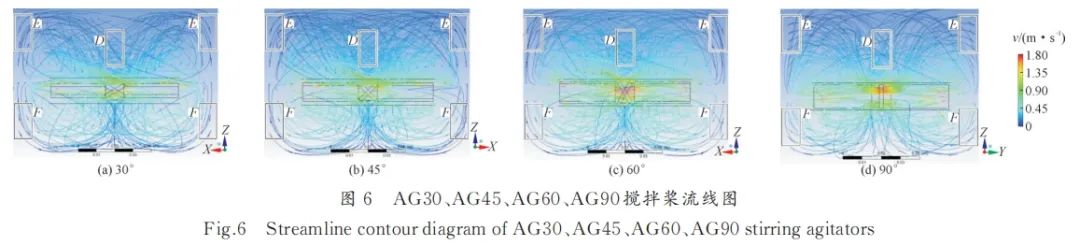图6

将图6的三维流线图投射在中心平面上，得到平面流线图，见图7。可以看出，AG30、AG45、AG60在区域形成了流场相互交汇产生的平面，即交汇面（Intersection surface，IF）。IF在图中与水平方向形成了一个角度，即混流角（Chaotic Fluid Angle，CFA）。AG90的CFA角度为0，即AG90不存在CFA，也不存在G区和IF。从整体与局部流线图分析，发现AG45混乱程度最大。AG30与AG90熔体流线混乱程度大致相同；AG45、AG60的流线混乱程度增加。AG30、AG45、AG60存在IF和CFA，AG90熔体流动过程中则无上述现象产生。

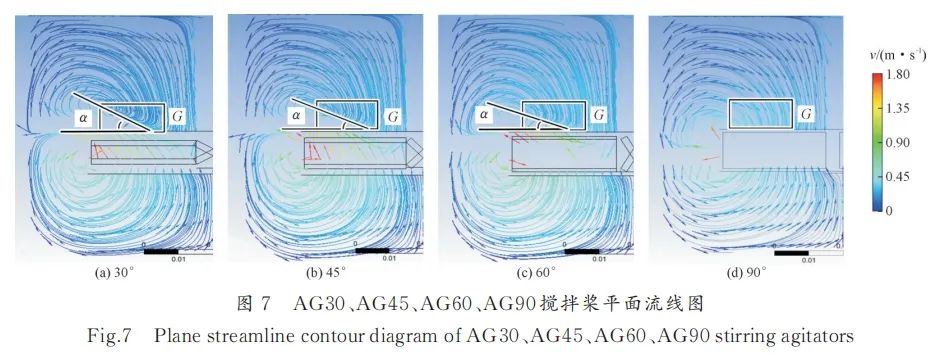图7

2.4 颗粒在熔体流动过程中的分散规律

对颗粒受搅拌器（桨杆和桨叶）作用不同时间下的空间位置进行模拟，结果见图8，其中红色为尚未受到搅拌器作用的表面颗粒群（搅拌初期），蓝色颗粒为受到搅拌后进入相对稳定状态（搅拌末期）的颗粒群。在0 s时，颗粒还未受到搅拌作用，因此表面颗粒群皆为红色，见图8a～图8d；当搅拌至5 s时，AG30、AG45、AG60表面颗粒已受到卷流作用而内旋至桨杆处，但AG90表面仍有未向中心汇聚的颗粒，见图8e～图8h。在颗粒分散进行至180 s时，颗粒分散进入相对稳态，见图8m～图8p。此外可以看出，AG30颗粒分散区域小，即受搅拌器作用范围小。代表稳态的蓝色颗粒占比从高到低排序为：AG30＞AG60＞AG45＞AG90。

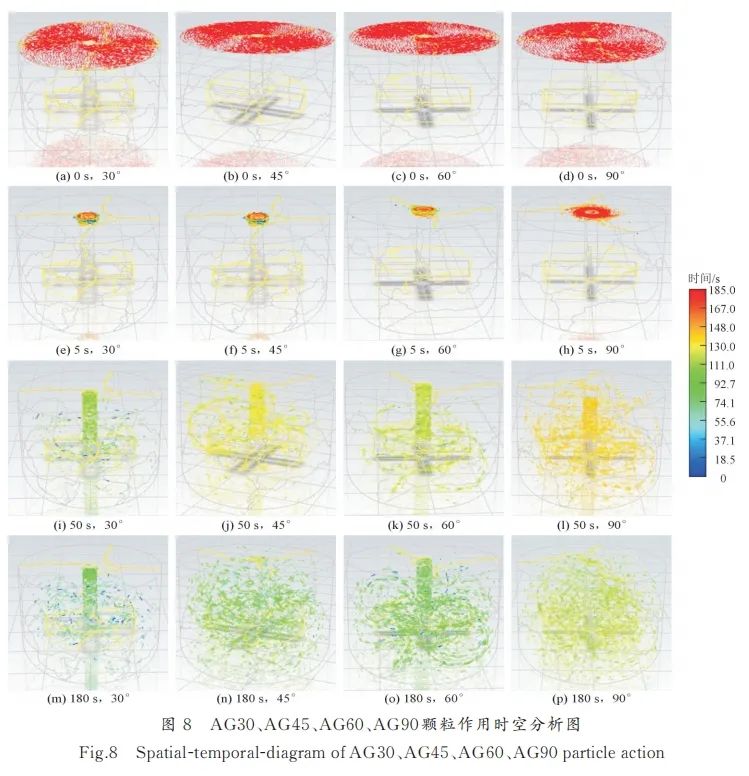图8

3 分析与讨论

3.1 熔体的流动行为

随着搅拌桨叶角度θ的增大，熔体高速区占比逐渐增加，而低速区占比逐渐减少。这是由于搅拌桨角度的变化会导致桨叶对流体的作用面积不同，见图9，该面积可由S=DLsinθ表示。当θ＜90°时，随着θ值增加，sinθ增大，作用面积S增大。此外，搅拌流型主要包括轴向流、径向流、切向流3种形式［35］，轴向流型主要动力来源为FN=Fcosθ，径向流型主要动力来源为Fr=Fsinθ。而桨叶角度θ的增大，使得桨叶对熔体的轴向流效应减小，径向流效应增大，径向传递给熔体的动量损耗减少。径向流主流向与搅拌作用方向在一个平面内，所以熔体流速的主要影响流型为径向流。闫禹伯［16］、潘荣选［36］采用FLOW-3D软件比较了15°和30°搅拌桨的模拟情况，发现随着桨叶角度减小（搅拌桨倾斜角度的增大），熔体运动逐渐以轴向流为主，径向流逐渐减弱，整体速度逐渐下降，验证了研究结果。从熔体整体速度分析可知，AG90的颗粒分散效果最好。

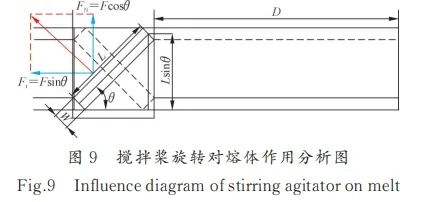图9

熔体整体速度分布至关重要，其轴向速度分布也同样具有规律性。随着距底部高度的增加，熔体流速呈现先增加后减少的趋势，近桨区熔体流速快，远桨区熔体流速慢，此规律不受桨叶角度的影响，这与黎义斌等［22］、MALUTA F等［37］和李青云［38］的研究一致。产生这一现象主要原因是由于近桨区熔体受到桨叶直接作用，速度提升明显，镁合金熔体属非牛顿流体，与水等牛顿流体相比具有更高的黏度、密度、湍流耗散率等物性参数［39-44］，导致远桨区的熔体受桨叶影响大幅衰减。因此，近桨区熔体速度与远桨区熔体速度存在明显差异。

随着搅拌桨桨叶角度的增加，其熔体轴向速度梯度增大，可归结为：①AG90熔体速度基数大，桨叶影响范围小，远桨区能量耗散大，导致近桨区与远桨区差距明显；②斜叶桨桨叶影响范围大，对远桨区熔体存在较明显的轴向效应，因此远桨区与近桨区速度差小。研究表明，熔体速度对颗粒分散至关重要。RAVE K等［45］比较了靠近桨叶区域与远离桨叶区域增强相的分散情况，发现距桨叶近的区域，增强相分散容易；远离桨叶靠近熔体表面的区域增强相团聚明显。此外，徐跃等［46］也发现，搅拌桨桨叶角度的增加会使得熔体中心速度梯度变大，进一步增强了区域熔体的剪切作用，促进了增强相的破碎，而速度梯度的增大可以改善颗粒分散效果［47］。综上，从熔体整体速度、轴向速度梯度综合分析，AG90颗粒分散效果最好。

AG60熔体矢量混乱度最大，更利于颗粒分散；AG90搅拌桨对熔体的轴向推动效果差，熔体矢量混乱度小。造成直叶桨与斜叶桨混乱度差异的原因在于，90°直叶桨桨叶呈对称结构，不考虑重力、浮力等的影响，旋转产生的涡流流场在近桨区两侧也呈对称结构；而斜叶桨打破了这种对称性，其桨叶会产生轴向分力FN，见图9。陶辰亮［48］针对斜叶桨和直叶桨进行矢量图模拟，发现在近桨区熔体受桨作用有明显的轴向运动趋势。但根据FN=Fcosθ可知，桨叶角度越小则轴向分力FN越大，故在模拟的4组角度桨叶中，AG30轴向作用应最为明显，高速轴向流体（HSAF）向上最为密集。然而，模拟表明，桨叶角度为60°时HSAF最密，这是源于桨叶角度为30°时径向力过小，熔体动能小，从而导致流体整体速度偏低，非牛顿流体黏度、耗散率高［39-44］，导致HSAF数量锐减。因此，从熔体矢量与HSAF密集程度分析，AG60分散效果最好。

图10为直叶桨与斜叶桨二维流场流型。从流动行为角度分析，熔体因受坩埚外壁的限制，在桨叶径向效应作用下高速冲击坩埚壁。一方面，熔体会发生少部分反射和大部分的沿壁流动［49］；另一方面，根据伯努利流体原理［50］，搅拌桨在径向排出熔体的同时，会造成该位置压力降低，使得靠近桨叶的上下方熔体对该位置回流补充。以上两方面使得熔体流动构成了一个完整回路，也是搅拌作用下熔体的主要回路——双环型回路，见图10a。斜叶桨的轴向效应相对径向效应而言程度稍弱，但是在主要回路双环型的基础上，这部分轴向效应存在的重要作用是使得双环回路的内环侧贯穿，使其形成单环型回路，见图10b，这与黎义斌等［22］、陈美辰［51］和PARVIZI S 等［52］在搅拌桨类型所产生的流型方向研究一致。双环型回路作为基础流型，同时存在于4组搅拌过程中。其中，直叶桨流场中主导流型是径向流，搅拌桨不产生轴向分力，在AG90熔体中不存在内环贯穿效应，这使得双环型流型成为直叶桨的主导流型也是最终流型。斜叶搅拌桨组会在此基础上多增加一种搅拌桨轴向力产生的局部循环来将双环连接为单环，使其最终流型为单环型回路。

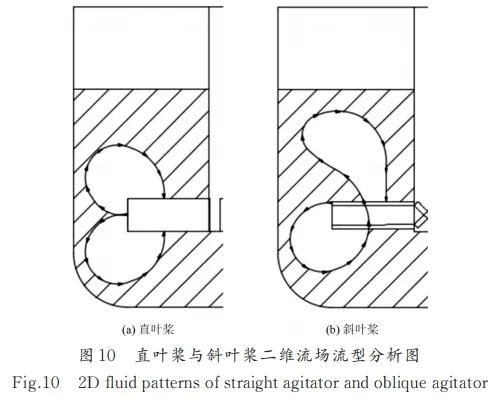图10

从流型相互转化角度看，RAVE K等［53］认为，在一定流场条件下，同一种搅拌桨不同旋转速度也会产生不同的流场。随着搅拌速度增加，流场会逐渐从双环形过渡到单环形，该研究完善了搅拌桨参数对流场流型的影响。从流体行为对颗粒分散的角度分析，双环型流场下的流体运动保持高度对称，会产生多点交汇现象，导致颗粒在该点会产生对冲趋势形成瞬稳态，从而导致运动速度大幅减小，不利于颗粒分散；单环型流场凭借斜叶桨的设计，打破了这种相对静止的瞬稳态，将双环型流场贯通为单环型流场，使得颗粒在受到熔体影响的同时，能够以一个较为整体的无死角的运动在熔体中分散开，相对直叶桨而言死区效果改善明显。因此从流场流型上看，斜叶桨的搅拌效果更好。综上，从流型角度分析，AG30、AG45、AG60搅拌效果更好。

斜叶桨能够在熔体流动过程中产生交汇面IF和混流角CFA，这主要源于斜叶桨对熔体轴向的推动作用，熔体在旋转过程中会存在向上分流的趋势，与另一部分相对稳定的熔体产生交汇，形成流线较为集中的G区域，进而在流线剖面图上形成一个IF。流线集中区域代表着熔体携带颗粒集中流经处，碰撞效果显著，有利于提升颗粒分散效果［54-55］。另一方面，任意给定区域内流线混乱程度的增加，使得该区域熔体中颗粒运动的一致性降低，即任意给定区域内相同数量的颗粒在流经该点时会具有更多样的运动方向。熔体流动行为直接影响颗粒的分散，IF和CFA会使得颗粒产生更加多向化的运动趋势。因此，从流场流线以及IF和CFA影响角度分析，AG45的搅拌效果较好。

3.2 颗粒的分散行为

搅拌过程中，颗粒运动的过程可分为3个阶段：颗粒团随熔体运动-桨叶撞击颗粒-颗粒分散回归熔体［56-58］。搅拌桨主要有两大作用：一是影响熔体流动行为，带动颗粒实现分散。由于熔融状态镁合金具有较高的黏度，严重限制了颗粒的分散，在半固态搅拌过程中可通过提高熔体旋转速度，增大剪切力，以改善颗粒的团聚现象。但熔体运动是一个时间相对较长且分散相对不均的过程，随着时间延长，颗粒与颗粒之间相互碰撞增加了聚集的概率。因此搅拌桨第二个作用就是在颗粒聚集一定程度后，对颗粒进行高速冲击并为颗粒的分散提供能量，从而提高分散效率，减少团聚现象。

图11为颗粒增强相均匀加入到流体表面后的分散剖面图。可以看出，搅拌对表面颗粒运动轨迹的影响可以分为两个阶段：第一阶段，遍布表面的颗粒发生内旋，开始向桨杆附近聚集（图11a～图11h），直至表面只有桨杆附近有较薄一层颗粒，至此第一阶段结束（图11i～图11l）；第二阶段，该部分颗粒沿着搅拌杆向搅拌桨中心低压区旋转下降，触碰到高速旋转的桨叶时发生撞击而被分散（图11m～图11t），直至该部分颗粒全部被打散，至此第二阶段结束（图11u～图11x）。

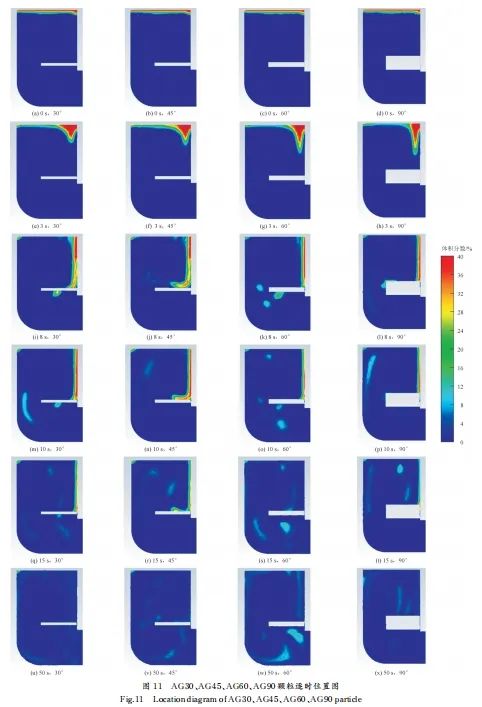图11

图11中蓝色颗粒的数量越多，颗粒受到搅拌器作用进入分散末期的颗粒越多，颗粒分散效率越高。因此可以得出颗粒分散效率顺序为：AG30＞AG60＞AG45＞AG90，但AG30搅拌桨对颗粒影响的范围较小。其原因在于，AG30搅拌桨轴向分力过多，导致整体速度情况不好，因此其旋转搅拌所能影响到的颗粒范围相对AG45、AG60搅拌桨组要小得多。从颗粒分布结果看，AG60颗粒分布最好，这是因为从速度角度考虑，AG30的桨叶搅拌速度不够，因而影响了分散效果。从矢量与流型角度考虑，AG90桨叶形成的双环形不利于颗粒分散，且HSAF数量少。从流线角度考虑，AG90不存在IF和CFA，混乱度低，颗粒分散效果不好。AG45和AG60没有明显缺陷项，且AG60在速度、矢量、效率方面好于AG45，因此颗粒分散效果最好。

结 论

（1）搅拌熔体高速区面积与桨叶角度增长呈正相关，AG90熔体整体速度最大，轴向速度梯度最大。搅拌桨桨叶角度的变化不会影响熔体速度轴向分布情况。

（2）斜叶桨搅拌产生的流型为单环型，直叶桨搅拌产生的流型为双环型。从减少死区的角度分析，单环型流型要优于双环型流型；从颗粒分散角度分析，斜叶桨搅拌效果要好于直叶桨。

（3）斜叶桨在搅拌过程中可以在熔体中形成交汇面（IF），其与水平面产生的混流角（CFA）α大小与桨叶角度增加呈负相关。IF能够提升熔体混乱程度，有利于颗粒分散。混乱程度增大，颗粒在流经该点时运动方向更多，分散效果更好。

（4）从颗粒分散结果可得，在分散效果较好的30°、45°、60°等3组斜叶搅拌桨组中，随着搅拌桨桨叶角度的增大，颗粒分散效果提升，其中60°斜叶搅拌桨颗粒分散效果最好。

参考文献

向上滑动查看更多

来源：《特种铸造及有色合金》 2024年第6期

郭子义，邓坤坤，聂凯波，等. 颗粒增强镁基复合材料流体行为与颗粒分散的数值模拟［J］. 特种铸造及有色合金，2024，44（6）：781-790.

GUO Z Y，DENG K K，NIE K B，et al. Numerical simulation of fluid behavior and particle dispersion of particle reinforced magnesium matrix composites［J］. Special Casting & Nonferrous Alloys，2024，44（6）：781-790. DOI：10.15980/j.tzzz.2024.06.010

免责声明：中国复合材料学会微信公众号发布的文章，仅用于复合材料专业知识和市场资讯的交流与分享，不用于任何商业目的。任何个人或组织若对文章版权或其内容的真实性、准确性存有疑议，请第一时间联系我们。我们将及时进行处理。

继续滑动看下一个轻触阅读原文

中国复合材料学会向上滑动看下一个

原标题：《【复材资讯】颗粒增强镁基复合材料流体行为与颗粒分散的数值模拟》

阅读原文