“约当定理“携手“鸽笼法则”可演绎证明四色猜想成立

四色猜想最先由格斯里（Francis Guthrie）于1852年提出，他是南非数学家，在英国读大学；另一说法，四色猜想是由德国数学家莫比乌斯（Mobius）于1840 年提出。四色问题的内容是“任何地图不同色相邻区分四色足够”。题面很简单，数学工作者却用了120多年才勉强解决了它，且证法超常规。1976年美国数学家阿佩尔和哈肯须借助计算机完成上百亿次验算才证实了那些特殊的情形时的四色猜想也成立。计算机辅助证明可分为两大类，一类是验算可穷举部分，一类是验算可递推部分。人工证明环节就是将无穷部分能逻辑地降为有穷部分和可递推部分。

直到降为可由1、2、3等初项和后继项推出。可惜人工环节不能持续简化下去，只能“愚公移山”靠“暴力穷举”，这令很多数学家们大为不满，好比小学生做应用题，能报出正确答案，可就是列不出算式。但阿佩尔和哈肯乐观预言，不用“暴力穷举”，标准证明四色猜想将由中学生完成。可见四色猜想的证明一定存在初等的逻辑推理证法。一旦发现可人工逻辑证明，人类便能快速完成不同类相邻着色，能深刻理解最核心的造型结构是什么，如此将为计算机的发展能提供重要的基础数学理论支持。

01. 数学发展不能停留在计算机辅助证明上

哈肯证明四色猜想中的有限图部分用暴力穷举完成虽是有效的，但确实象一本电话簿，而不象一首诗。导致很多读者误以为计算机暴力穷举证明的部分直接就是无限集，如果真是那样则定是无效证明。那么多数学家检验过了，不可能有违普通常识，这是不用怀疑的，要担心的是分类如此复杂

，有没有因漏项导致出现误证。阿佩尔和哈肯所得到的1936种有限情形，是通过489种规则可任意给出的上百亿幅地图，利用“放电法”，经计算机统计归纳得出的有限简化结果，这是可理解的，但是否仍有小错还不得而知，因为“暴力穷举”完成的目标实在太大了，无法让更多数学家们能在短时间里作出判定。既然相信分类情形是有限的，它的排列组合也必是有限的，其有限部分被暴力穷举证明当然是有效的。问题是他的可穷分类来源不能继续简化，这就不能阻止人们会难免怀疑：到底是哈肯的规则在产生任意图，还是哈肯的规则在产生随机图。随机图是概率图，是不能替代任意图的。递推是否是紧邻的，分类是否是可穷的，这些都需要检验。总之，得让所有数学家们在短时间内能够理解，才算是一个漂亮的证明。还记得冯 • 诺依曼（John von Neumann）的随机图生成器吗？乌拉姆（Ulam）发明了用蒙特卡罗方法（Monte Carlo Method）来做概率逼近证明，但该方法只能用来证明物理定律，不能用来证明数学定理。数学归纳法要求可穷分类，而不是逼近分类。因为数学定理都是用全称肯定判断来描述的。也就是说因程序底层设计不完善计算机证明是存在错误风险的。

退一步而言，即便计算机完成了证明，人类对内在变化过程的理解仍处于无知状态。阿蒂亚（Michael Atiyah）曾说过：“我们的理想是探究数学真谛，而不是利用机械执行指令的计算机推演论证。”另一位菲尔兹奖获得者泽尔曼诺夫（Zelmanov）也表示赞同：“只有所有数学家都认可的证明方法才是真正有效的，所以我对机器证明方法的前景并不看好。”他说的有道理吗？如果数学证明方法只有生成它的机器能够理解，我们真的可以相信吗？

笔者还是选择了愿意相信，当年希尔伯特率先使用存在性证明时，也遭到了很多人非议，计算机辅助证明横空出世也会一样。只是人类不要停留在计算机辅助证明上，要选择继续纯人工逻辑地完成存在性证明和构造性证明。如此这般，一可检验计算机证明是否有错其底层算法是否矛盾，二是如果正确也便于人类深度理解内在的变化过程。如此数学才会有进步。丘成桐说，人工智能尚缺基础数学方面的理论支持，印证该说法的就是计算机辅助证明能做成的事，人工证明却完成不了。我们在设计人工智能的时候是知其然但不知其所以然的。

02. 肯普证明四色猜想的漏洞真的不可弥补吗？

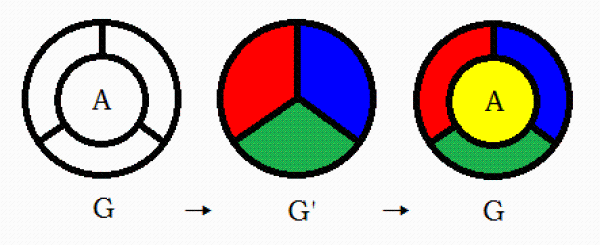
肯普是个律师，证明四色猜想取得重大突破是从肯普开始的。四色猜想的证明一开始就是“外行”在主导完成证明进程，难怪哈肯说，四色猜想的人工证明完全有可能被中学生拿下，因为这是一片处女地，解决它的机会对不同角色者的机会均等，可用到的已知条件并不复杂，一些奇思妙想完全有可能带来意想不到的进展。肯普建立了“不可避免集”和“可约构形”的思想。简单地说，任意给定的平面地图，可分成已着色部分

（即由四色互不相邻的两类肯普链构成），以及未着色部分，只要证明未着色部分与邻接色存在诸如“d(v)=2、3、4、5”这样的构形，即2度，3度，4度，5度的“不可避免集”，就可继续完成四色互不同类相邻，肯普成功完成了这项证明。于是2度图，3度图，4度图，是很显然可区分的，其中5度图（即5条边共一个顶点）能不能完成四色互不同类相邻呢？一般是可以的，碰上邻接色不可以时，对已着色图经过部分国家“换色”也是可达成目标的，于是未着色部分就成了“可约构形”，如果“不可约构形”存在，就一定存在“最小5度图”，肯普证明5度图总是可约的，于是“含最小5度图的不可约图”就不存在，于是所有的“不可约构形”就不存在，如此就证明了四色猜想成立。肯普的思路是不是很妙？数学界于是就把猜想变成了定理，可惜多年以后杀出个希伍德，又把定理变回了猜想。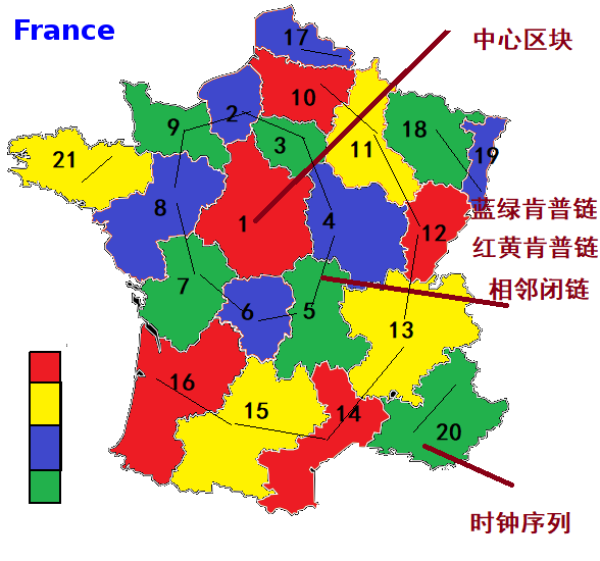

希伍德根据肯普的证明思路构造了一个有25国的反例，希伍德发现二次连续“换色”时无法做到不撞色，也就是说一次静态区分能成，多次动态区分就做不到同色不相邻了。希伍德的反例不是四色猜想的反例，是肯普证法的反例，他使肯普的四色猜想证明落空了，但四色猜想并没有证否。希伍德也没有完全抹杀肯普的成果，根据“不可避免集”，存在五色图总是可约的，于是用数学归纳法证明得到了五色定理。希伍德的反例，肯普无法解决。根据希伍德的说明，肯普的错误在于证明5邻国是可约构形时，构造两条肯普链以换色，然而第二次换色时，肯普的方法并不总是成功的。希伍德提供一个包含25个国家的地图作为反例。希伍德的报告是由肯普自己提交给伦敦皇家数学学会的。肯普承认自己的证明中存在缺陷，并且他未能去除这个缺陷。

肯普并未完成超限数学归纳法中的相邻迭代环节的推理证明，只完成了某个特例的一次“换色”，没有完成任意后继相邻都可成功“换色”，因此肯普和希伍德都没有彻底理解四色足可区分平面的规律。直到用互异肯普闭链相邻迭代构造任意平面图才算正确理解了四色猜想，用互异肯普闭链的链数与自然数一一映射才算完成了超限数学归纳法的逻辑构造。这是本文作者在四色问题上的一次原创突破。

只有真正理解区分地图四色足够原理，才可快速完成不同类相邻着色，才能深刻理解平面世界里的最核心的造形结构。仅凭这一点就给计算机发展提供了很重要的基础数学理论。证明四色猜想的过程也分筑基和封顶两部分，筑基部分用重合法的数学工具，证明了“每条闭链不超过三色足够区分”的引理成立，同时用约当定理还证明了所有的闭链构成了子树遍历序列（前序遍历即树叶序列）；封顶部分用相邻论的数学工具，证明了“两两相邻闭链不超过四色”的引理成立，同时用鸽笼原则证明了一邻单区块总能被相邻闭链中某区块全覆盖，故互异相邻闭链能成功紧邻延申。其中筑基部分满足“若尔当（Jordan）曲线定理”，可构造子树遍历序列（树叶序列），从而可用超限数学归纳法证明四色猜想。其中封顶部分可满足“鸽笼法抽屉原则”，三色足以区分邻接色的引理就是用顶点度数判定法和侧边点数判定法来完成证明的。一旦能确定邻接色周期（即肯普链或肯普链加单区块），有了它就有了结构可延拓可递推的模型。

 03. 用“三色可约图”来替代肯普的“四色可约图”和希伍德的“五色可约图”

在肯普的基础上证明四色猜想要做的改进其实并不多。首先在定义可约图上须改进下，什么叫可约图呢？凡与邻接色相邻的未着色图能用不超过三色的“肯普闭链”或“肯普链+单区块所构成的闭链”区分即谓可约图。该着色法永远保留每次邻接色皆不超过三色。该定义同肯普和希伍德的可约定义有所不同，肯普是四色可约图，希伍德是五色可约图，本文作者完成四色猜想的证明用的是三色可约图，这是最为本质的区别。如此一改进，就解决了大问题。希伍德的反例证明了，肯普的邻接色为“四色可约图”是不能完成二次迭代的，但换成“三色可约图”就不一样了。

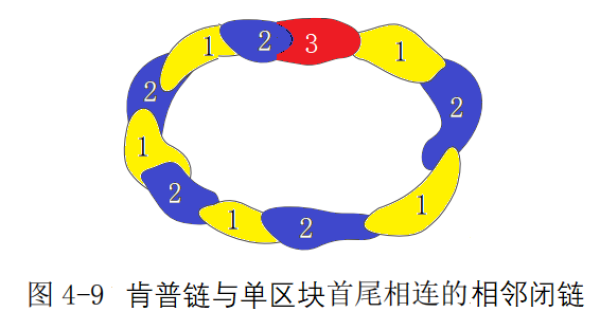
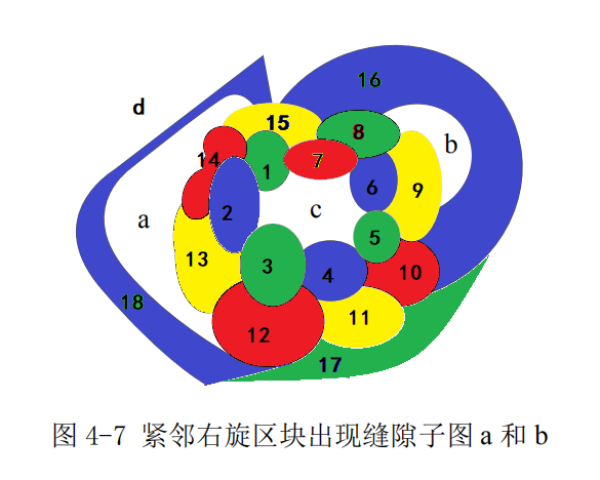
以法国大区图来说明，1号区为中心区块，中心区块一经确定，给定图的区块时钟序列就确定，所有的区块都有唯一编号了，这个思想非常重要，它意味着不同中心的两种语言A和B，只要知道A和B之间的间隔，两国语言就可以全部翻译出来，这才是计算机的底层算法思想。互联网上的信息就是一张大网页，它所对应的序列有唯一确定性非常重要。为何可用超限数学归纳法证明四色猜想就指望它了。任何一个给定图，都可以用若尔当曲线来一分为二，假如中心区块为若尔当曲线，那曲线内的区块数为0个，曲线外的区块数为无穷多个。

再以图4-7来说明，“1-2-3-4-5-6-7”闭链区块是由蓝绿肯普链+红色单区块构成的，“7-15-14-13-12-11-10-9-8”闭链区块是由红黄肯普链+绿色单区块构成的，说明若尔当曲线一分为二，有四种可能，内无外有，内有外无，内有外有，内无外无，由闭链构成的若尔当曲线，不断连接下去是可以充满任意给定地图的。而每次相邻闭链不是肯普链就是肯普链加单区块。由于单区块每次覆盖的图都不超过三色，故总是能用第四色来填充，因此，邻接色不超过三色的后继相邻闭链总能三色区分。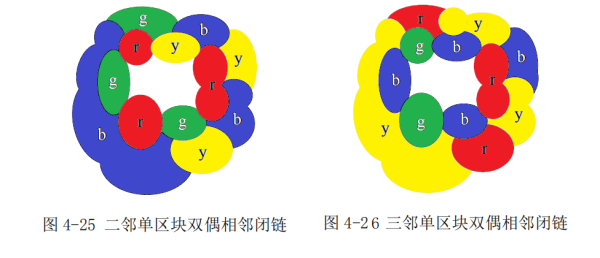

如此任意给定图就都可以迭代用不超过三色的相邻闭链不断向未着色图延伸。在构造相邻闭链时难免会出现a、b、c、d等未着色地图的情形出现，但每次产生这样的子图都是邻接色不超过三色的，而邻接色不超过三色的子图，从单区块出发构造一个相邻闭链，要么是肯普链，要么是肯普链加上一个单区块，而单区块是可以用第四色来区分的。更重要的一点，单区块可由鸽笼定理来确定总存在被后继或前继相邻闭链中的某一区块全覆盖，故相邻闭链能成功向内外未着色区迭代推进。如此未着色区就不存在“最小可约图”。四色猜想获证。

四色猜想能够成立的核心原因就是，任意给定地图都存在用“若尔当曲线”构造出的“子树遍历序列（前序遍历，即树叶序列）”，有了这样的序列就能使每条相邻闭链成功地与自然数一一映射了，这是可以合法使用超限数学归纳法的原因。然后就是相邻闭链的奇偶区块数色性区分最多不超过三数，根据这一性质于是都能被后继相邻闭链中的单区块用第四色或某一区块全覆盖，这个性质甚是奇妙，这是能证明四色猜想成立的关键。可见完成证明核心是“若尔当曲线构造出了子树遍历序列”，关键是“由肯普链加单区块构造的两相邻闭链存在互异覆盖”。因两类肯普链是全互异的，故彼此的单区块也就能互异选取，尤其是每次取相邻闭链总是从共用前继的单区块开始，故后继一色或二色或三色总能覆盖前继一色或二色或三色，这是四色猜想能够成立的深层原因。

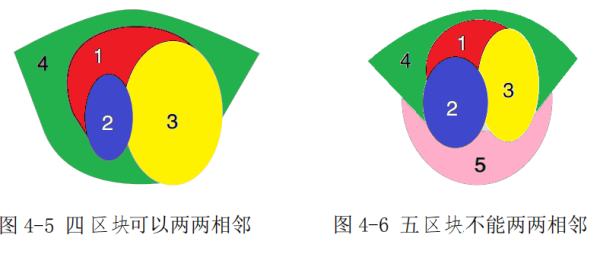
这个证明是可以满足直觉理解的。图4-5是“四邻定理（即五个区块之间不能两两相邻定理）”，即四区块的紧邻图可以两两相邻，区块数大于四的紧邻图就不可以两两相邻。第四国要与第一、二、三国两两相邻，必至少要全包围一国，不是左包围，就是右包围，如此至少总有一个国家被全包围，否则就无法相邻，故五区块定不能两两相邻。该性质说明了，只要区块数不两两相邻，就用不着添加新颜色来区分，第5色可以用第1色替换。如此就说明了第五区块是可约图。它在邻接色不超过三色的条件下，第五区块总是可约恒成立。因为它总能用第1色替换的方式可约，第五区块部分可约后，其邻接色继续保持不超过三色，可约操作可迭代进行。敏感的人仅凭这就知道四色猜想已获存在性证明。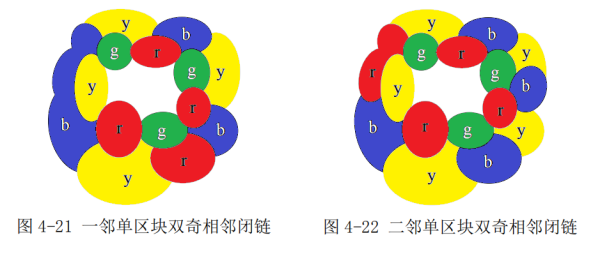

我们之所以设计邻接色不超过三色，就是为了未着色图能成功可约，在此思路下，我们还成功证明了，肯普链加单区块的邻接色是可以成功延伸互异肯普链的，为了相邻封闭有时不需要加单区块，有时候需要添加单区块。

  04. 每条闭链不超过三色足可区分，相邻闭链则四色足可区分

为了确保四色猜想的纯人工逻辑证明是可靠的，我们再开辟一条证法。也就是证明相邻闭链定理是成立的，这条定理是这样刻画的：每条相邻闭链不超过三色足可区分，两条相邻闭链则四色足可区分。

因为任何一条闭链，要么区块数是偶数，要么区块数是奇数，偶数是可以用肯普链来刻画的，奇数是可以用肯普链+单区块来刻画的。如果说一阶肯普链可产生线条，那么二阶肯普链则能可产生平面，暖色红黄肯普链看成一个区块，那么冷色蓝绿肯普链则可看成另一个互异类的区块，如此紧邻地交替相连就构成二阶肯普链。相邻闭链定理就是一个二阶冷暖色不断重复的肯普链。

因为根据若尔当曲线定理可判定，任何给定地图都是可以用若尔当曲线区块闭链的结构来充满的，故平面图的内部结构关系就是前继闭链与后继闭链的新型线性关系，说白了平面图就是一个二阶肯普链，故它满足高维空间区分数公式f（n）=2^n，当n=2时就是四色猜想，而n维空间，可由n阶肯普链来区分。只是这个二阶肯普链不是简单的一根绳子，而是一棵树，这棵树上的树枝用时钟序列来重组，是可以连接成一根绳子的。故这棵树等价一根绳子，绳子上的纽结就是绳文，绳文可以映射宇宙中的所有信息。只要开放算法，很多不可数集就能不断被策反到可数集中去。

每次邻接色上的一条闭链为何三色足可区分？二条相连闭链为何四色足可区分？

因为一条闭链的区块数不是奇数就是偶数，偶数可用肯普链区分，不超过三数，奇数也可用肯普链区分，再外加一个第三色单区快，其中偶数闭链也可以用肯普链，再外加一个单区块来构造，可见任何一条闭链三色足可区分。由于包围每次邻接色的闭链，根据鸽笼定理，相邻闭链之间总有单区块被后继或前继相邻闭链中的某区块完全覆盖，故三色区分工作可用互异肯普链来迭代完成。

在此基础上那二条相连闭链为何四色足可区分就好证明了，可以定义每次的后继相邻闭链总是从前继相邻闭链中的单区块开始的，如果前继肯普链是暖色的话，那么后继肯普链就是冷色的了。如此构成的紧邻闭链不是偶数封闭就是奇数封闭，其中偶数封闭就是一条冷色调的肯普链，包围了所有的暖色，如果是奇数封闭就需要再添加一个单区块，而前继闭链只有暖色和第三色，后继闭链定是冷色且覆盖了部分暖色，最后区块会邻接三色或二色或一色，故能启用第四色就足够。相邻闭链之间的关系，可用鸽笼定理来分析。

相邻闭圈区块链除了奇偶关系外还存在四种可穷分类，是根据侧边上的顶点个数不同来区分的，这就是侧边点数判定法。以下就用侧边点数判定法来证明后继相邻闭链能够全部覆盖前继闭链中的所有第三色，仅用互异肯普链和前继肯普链中被覆盖的其中一色。

1. 外包围区块链在公共边界上的顶点个数与内包围区块链在公共边界上（即相邻闭链上的邻接线）的顶点个数不等。

A. 外包围区块链在公共边界上的顶点个数大于内包围区块链在公共边界上的顶点个数。若 x上的顶点数 V（x）＞ y 上的顶点数 V（y），根据鸽笼原理，必有其中一个内包围区块边界 x 上的 V（2）∈ y 上的 E（1）。故存在内包围后继区块可用肯普链延拓。

B. 外包围区块链在公共边界上的顶点个数小于内包围区块链在公共边界上的顶点个数。若 x 上的顶点数 V（x）＜y 上的顶点数 V（y），根据鸽笼原理，必有其中一个内包围区块边界 y 上的 V（2）∈x 上的 E（1）。故存在外包围后继区块可用肯普链延拓。

2. 外包围区块链在公共边界上的顶点个数与内包围区块链在公共边界上的顶点个数相等。

C. 外包围区块链在公共边界上的顶点个数等于内包围区块链在公共边界上的顶点个数。若 x 上的顶点数 V（x）=y 上的顶点数 V（y），且 x 上的 x-a 与 y 上的 a 共边在相应段上，即 V（x-a）＞V（a），V（a）＜ V（y-a），根据鸽笼原理，必有其中一个内包围区块边界 y 上的顶点数 V（2）∈x 上的边数 E（1）或 x 上的顶点数V（2）∈ y上的边数 E（1）。故存在内包围或外包围后继区块可用肯普链延拓。如此单区块必会被一色、二色（含肯普链）或三色（含肯普链加单区块）包围，。

D. 外包围区块链在公共边界上的顶点个数等于内包围区块链在公共边界上的顶点个数。若 x 上的顶点数 V（x）=y 上的顶点数 V（y），根据一一映射，必有其中一个内包围区块边界 y 上的顶点数 V（1）∈x 上的边数 E（1）或 x 上的顶点数 V（1） ∈ y 上的边数 E（1）。故存在后继区块链可用肯普链延拓。

总之，外包围区块链在公共边界上的顶点个数与内包围区块链在公共边界上的顶点个数要么相等，要么不等。相等时要么全部对齐相等，要么不对齐相等，此时定有局部区域跟整体不等的情形一致。故仅对齐相等的情形可考虑二邻单区块的相邻闭链模式，而内外顶点可对齐的相邻闭链是不会遭遇“悔棋模式”的，如此就有依据可避开选择二邻单区块了，因为只有邻接线上内外顶点数完全对齐时，或偶数个区块相邻单区块时，才无法判定内外有完全被包围的单区块，其他情形根据鸽笼定理，定有单区块被奇数区块完全覆盖，如此相邻闭链就可迭代推进。

相邻闭链根据区块数奇偶性，区块数差异性，同第三色的三类相邻性，一共可穷分类为 64 种情形。其中 32 种无须针对第三色，直接在双色肯普闭链上后继添加闭链，这个很容易做到，称平凡链，难在另外 32 种。我们把非平凡链都设定为前继闭链有第三色才能区分，事实上奇偶型、双偶型是无须三色区分的，二色足够。

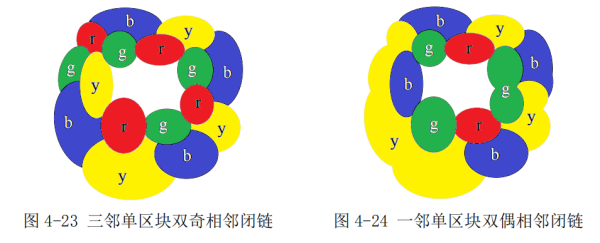
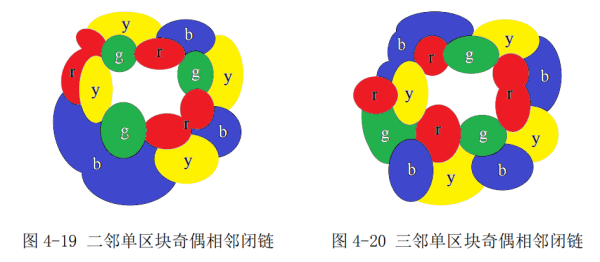
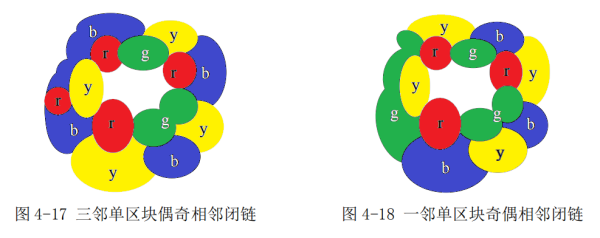
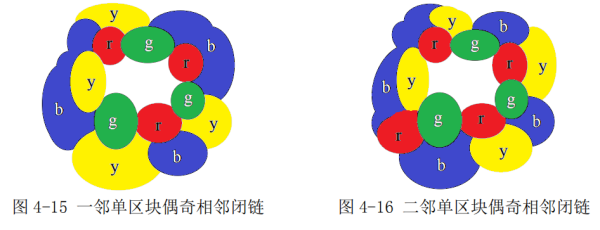
本文列举了 16 种情形，因为向内后继相邻与向外后继相邻是对称图，向外成立，向内就成立。而 16 种图里，12 种是一般情形，分一邻，二邻、三邻第三色单区块，对应偶奇、奇偶、双奇、双偶 4 类就有 12 种，其他 4 种是特殊情形，须启动“悔棋模式”，使其任意后继闭链不超过三色区分。二邻型可区分，2n 邻型即可区分，三邻型可区分，2n+1 型即可区分。我们从图4-15到图4-26中所分析的12种图，都清晰地证明了可四色区分的，且每一条相邻闭链都不超过三色。

须警惕的是二邻单区块、二邻多区块的情形，它对前继相邻闭链有要求，如果不符，要用“悔棋模式”调整色链齿轮周期，其他情形根据顶点度数判定法、侧边点数判定法即可找出相邻闭链上的第三色区块，使相邻闭链永远可三色区分。每次从单区块开始延伸找到的后继相邻闭链，可能是偶链也可能是奇链，如果是偶链，则后继相邻闭链是偶偶相邻闭链，如果是奇链，则后继相邻闭链是奇偶相邻闭链。在侧边点数、顶点度数对等或不对等的作用下，鸽笼原理成立，故总有单区块被其他三色全包围。于是每次可不超过三色完成封闭邻接色，并且一般第三色可设定为单区块，特殊时可调整为多区块。由于一邻第三色多区块可正常区分，能根据一般型派生出，可不列入特别型。而 n 邻第三色多区块可根据二邻第三色多区块同法依次派生，故省略不表。因此可将奇奇相邻闭链变换为奇偶或双偶型相邻闭链，即变成平凡型闭链。如此任意地图皆可完成四色区分。

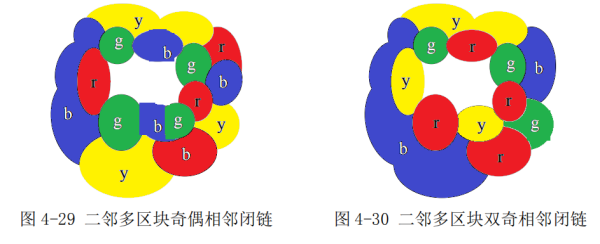
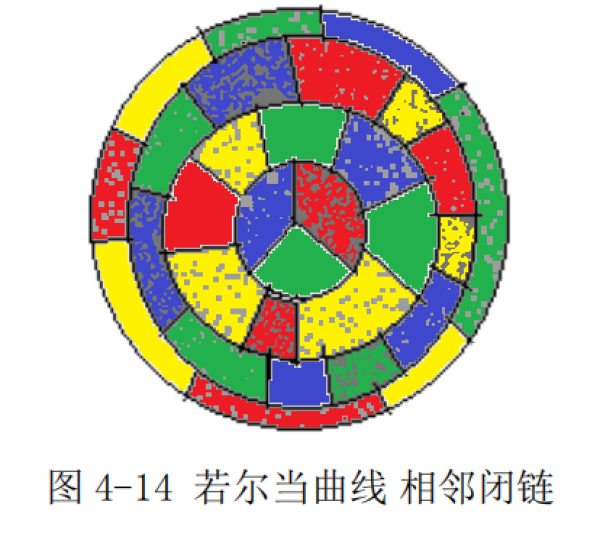二邻单区块会出现特殊情形（含2n个区块相邻单区块），会导致撞色，故图4-27到图4-30中分析了这种情形。遇到该特殊情形将要启动“模式悔棋”，就是肯普以来的数学家们常用到的那种将已着色图进行部分换色从而避免撞色。二邻单区块中的两个区块都覆盖三色时，就不可避免会撞色，因同时都要用到第四色，此时就要对已有肯普链进行调整，再设置一个同类单区块，如此对称性就瓦解了，于是撞色现象解除。使用“悔棋模式”证明四色猜想要证明一定能悔棋成功。二邻单区块会出现撞色，是因为相邻图出现在了对称环境中，这种对称性是可以消解的，除了多设置几个单区块外，还有别的办法，那就是把与单区块相邻的两区块，用三色隔离掉其中一个，从而产生新分布的的邻接色，这个方法比新增单区块更彻底，也就是说二邻单区块是可以不断成功消解的。图5-2分析了该类情形。

本文证明了除了一个特殊情形外须用二邻单区块，即完全对齐且错开的情形，其它对齐不错开的情形是可以一邻单区块的，另外对等但错开的情形可归入不对等情形，所有的不对等情形都是可以找到一邻单区块的，或者被一邻单区块，就是多区块与单区块相邻，其中包括偶数个区块与单区块相邻，该情形容易出现对称图而撞色，因此偶数个所产生的对称性需要瓦解掉，凡邻接色出现四色，都可以用三色闭链将第四色隔离，从而可保证奇数个区块与单区块相邻。该性质还可以用”四邻定理“来阐明，被三色包围的第四区块，隔离第四区块可保持邻接色不变。以上已证明，一邻单区块是可以顺利着色的，满足一条闭链可三色区分，相邻闭链可四色区分。奇数个区块相邻单区块也能满足着色条件。

为了避开使用“悔棋模式”，可设置成几乎不用二邻单区块和二邻多区块，实际上仅一种情形非得使用二邻单区块，且不会有“悔棋模式”出现，前文已有交代，这里再提及一下。只有邻接线上内外顶点数完全对齐或错位对齐时，才需要二邻单区块，其他情形顶点数皆不对等或局部不对等或对等未错开，此时根据鸽笼定理，都定有单区块被相邻闭链中的某一区块覆盖，或被相邻闭链中的单区块加肯普链覆盖。

以上证明了，凡被确定一邻单区块或被一邻单区块的相邻闭链，都是可以顺利完成着色的，满足一条闭链三色足够区分，相邻闭链四色足够区分。根据鸽笼定理，相邻闭链很容易确定不是存在一邻单区块，就是存在被一邻单区块，这两者都是可以满足相邻闭链的着色要求的。偶数个区块数相邻单区块时，可利用四邻定理消解一个或交换出一个，并保留邻接色仍为三类，这是必然可以做到的。

根据以上论述，四色猜想就可以完成封顶证明了。 

证明：①由闭链 M1构造的图 G1可四色区分（有限可列）。②由内向外添加紧致相邻闭链 M2构造的图 G2可四色区分（有限可列）。③再由内向外添加闭链 M3构造的图 G3可四色区分（有限可列）。④另由子树遍历序列（树叶序列）可知，从 M1到 Mn 可无漏无穷充满任意给定地图，故该序列的延伸与自然数序列的延伸一一映射。⑤现假设依次由内向外（或由外向内）添加紧致可三色足够区分的相邻闭链 Mn 构造出的图 Gn 可四色足够区分任意图，可三色足够区分相邻闭链。⑥那么根据相邻闭链定理，由内向外（或由外向内）添加紧致相邻闭链M（n+1）构造出的图 G（n+1）亦可四色足够区分任意平面地图，可三色区分每条相邻闭链。四色猜想得证。

 05. 四色猜想在非“暴力穷举”层面上获证意义重大

大凡能够读到这里的，相信一定能听懂我用更简单的语言陈述四色猜想的证明。该文证明所要用到的数学基础离中学生掌握的背景知识并无多大差别。没有学过鸽笼法也学过整体大于局部，用该公理可以替代鸽笼法；没有学过若尔当曲线定理也学过子集，补集和全集，照样可以无缝隙地分类。故本文的证明，没有超出中学生不能理解的范畴。

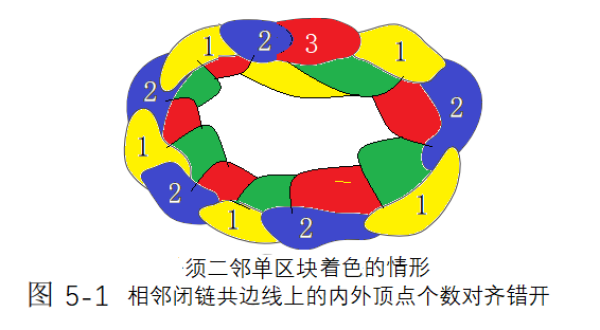1.一幅任意给定地图，都可以用相邻闭链填满，出现子图可依次填满。数学工具：集合论或若尔当曲线定理。2. 用肯普链或肯普链加第三色单区块构造相邻闭链，每条闭链不超过三色区分。数学工具：图形组合。3.在邻接色在不超过三色的基础所产生的相邻闭链亦可用三色完成区分。数学工具：鸽笼法或公理整体大于局部。相邻闭链之间必有一条交界线，比较交接线上内外顶点个数，结果有三种情形，内=外，内＞外，外＞内。相等情形用不超过三色可精准区分相邻闭链，要么是肯普链，要么是肯普链加第三色单区块，很平凡，这是须二邻单区块着色的情形，其他都能一邻单区块或被一邻单区块，如图5-1，单区块碰上与偶数个区块相邻，会碰上对称相邻，从而启动悔棋模式，将偶数个中的某区块隔离出去，从而消解对称性；不等情形，根据鸽笼法分配规则，必有两点或多点在相邻闭链的某区块内，故一定有单区块被相邻闭链中的某区块完全覆盖，故互异肯普链可以不撞色完成紧邻包围，如果是奇数，可添加单区块从互异肯普链中任选一色，单区块的位置由后继相邻闭链或前继相邻闭链的给定图确定。此外选择奇数个区块与单区块相邻也是可以人为选择闭链路径从而定能实现按条件延申闭链的。从而可避免碰上”悔棋模式“。

4.两条相邻闭链不超过四色区分。数学工具：图形组合。由于每条闭链不超过三色，有两条互异肯普链，这样就得到四色，而第三色单区块用的都是彼此互异肯普链中的颜色，并没有增添新颜色，故相邻闭链不超过四色可区分。5. 用相邻闭链迭代着色所有给定地图，显示四类着色足够。数学工具：超限数学归纳法。根据前面的地图结构分析，任意给定图，都是相邻闭链的延伸，并与自然数映射，故可用数学归纳法完成证明四色猜想。

四色猜想在非暴力穷举层面上获证，意味着人类真正理解了时间通过变速和拐弯是可以构造不同空间的，变速是构造一阶肯普链，拐弯是构造二阶肯普链，时间是可以储存和释放的。这是计算机的基本思想。庞加莱猜想获证说明了高维信息都落在球面上，四色猜想获证说明了网页信息都落在一根绳子上。哥德巴赫猜想获证说明了绳子上的所有信息都挂靠在蛇头蛇尾上，都在一阴一阳的连接关系上。四色猜想获证，说明了我们要学会从不同层面上去思考相邻关系。如果我们不能用若尔当曲线梳理出线性秩序，就不能使用超限数学归纳法证明四色猜想，就推广不了二阶肯普链；如果我们不能用鸽笼法规则找出全覆盖区块，就不能使超限数学归纳法中的递推关系成立，就不能处处可三色构造相邻闭链。可以说，是若尔当曲线定理和鸽笼法抽屉原则证明了四色猜想。由于单区块总能被后继或前继相邻覆盖，所以二阶肯普链能无漏构造。由于若尔当曲线能分割出子树遍历序列（前序遍历即树叶序列），所以二阶肯普链能无穷推进。

非暴力穷举证明四色猜想，终于让某些核心思想浮出水面。不能线性二项分割的事物是不存在的，中国阴阳思想是鸽笼法运用的典型代表，“二”要承载不能用“二”平分的东西，那么其一，就必有更多的担当，这就是阴阳有别的思想。万物都能够互异连接构造，这就是哥猜，不能互异线性连接构造的事物是不存在的。我们只知道线性属于非线性，想不到非线性其实属于开放的线性中。只要开放简单，就能囊括复杂。这就是四色猜想获证的最大收获。互异相邻可以完全不在时空中（哥德尔不完备定理），但又完全不离时空（相邻论和重合法）。本文根据作者数论专著《数学底层引擎相邻论和重合法》中的论文改写而成。（文/罗莫）